Scientific Workflow with HSSM¶

Welcome to the scientific workflow tutorial. This tutorial starts with a basic experimental dataset and we will inch from a very simple HSSM model iteratively toward a model that captures many of the main patterns we can identify in our dataset.

Along the way we try to achieve the following balance:

1. Illustrate how HSSM can be used for real scientific workflows. HSSM helps us with model building, running the stats, and reporting results.
2. Allow this tutorial to be used as a first look into HSSM, shirking conceptually advanced features that are discused in the many dedicated tutorials you can find on the documentation

Colab Instructions¶

If you would like to run this tutorial on Google colab, please click this link.

Once you are in the colab:

1. Follow the installation instructions below (uncomment the respective code)
2. restart your runtime.

NOTE:

You may want to switch your runtime to have a GPU or TPU. To do so, go to Runtime > Change runtime type and select the desired hardware accelerator. Note that if you switch your runtime you have to follow the installation instructions again.

Install hssm¶

In [1]:

# If running this on Colab, please uncomment the next line
# !pip install hssm

# If running this on Colab, please uncomment the next line # !pip install hssm

Download tutorial data¶

In [2]:

# # Data Files
# !wget -P  data/carney_workshop_2025_data/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/data/carney_workshop_2025_full.parquet
# !wget -P  data/carney_workshop_2025_data/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/data/carney_workshop_2025_modeling.parquet
# !wget -P  data/carney_workshop_2025_data/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/data/carney_workshop_2025_parameters.pkl

# # Presampled traces
# !wget -P  idata/basic_ddm/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/basic_ddm/traces.nc
# !wget -P  idata/ddm_hier/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/ddm_hier/traces.nc
# !wget -P  idata/angle_hier/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_hier/traces.nc
# !wget -P  idata/angle_hier_v2/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_hier_v2/traces.nc
# !wget -P  idata/angle_hier_v3/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_hier_v3/traces.nc
# !wget -P  idata/angle_hier_v4/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_hier_v4/traces.nc
# !wget -P  idata/angle_v5/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_v5/traces.nc

# # Data Files # !wget -P data/carney_workshop_2025_data/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/data/carney_workshop_2025_full.parquet # !wget -P data/carney_workshop_2025_data/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/data/carney_workshop_2025_modeling.parquet # !wget -P data/carney_workshop_2025_data/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/data/carney_workshop_2025_parameters.pkl # # Presampled traces # !wget -P idata/basic_ddm/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/basic_ddm/traces.nc # !wget -P idata/ddm_hier/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/ddm_hier/traces.nc # !wget -P idata/angle_hier/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_hier/traces.nc # !wget -P idata/angle_hier_v2/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_hier_v2/traces.nc # !wget -P idata/angle_hier_v3/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_hier_v3/traces.nc # !wget -P idata/angle_hier_v4/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_hier_v4/traces.nc # !wget -P idata/angle_v5/ https://raw.githubusercontent.com/lnccbrown/HSSM/main/scientific_workflow_hssm/idata/angle_v5/traces.nc

Start of Tutorial¶

Load modules¶

In [3]:

import hssm
import pandas as pd
import pickle
import numpy as np
import arviz as az
from matplotlib import pyplot as plt

import hssm import pandas as pd import pickle import numpy as np import arviz as az from matplotlib import pyplot as plt

Load workshop data¶

In [4]:

def load_data(filename_base: str,
              folder: str = "data") -> tuple[pd.DataFrame, pd.DataFrame, dict]:
    """Load saved simulation data and parameters from files.

    Parameters
    ----------
    filename_base : str
        Base filename used when saving files
    folder : str, optional
        Folder containing saved files, by default "data"

    Returns
    -------
    tuple[pd.DataFrame, pd.DataFrame, dict]
        Contains:
        - DataFrame with modeling data
        - DataFrame with full data  
        - Dict containing group and subject parameters
    """
    df_modeling = pd.read_parquet(f"{folder}/{filename_base}_modeling.parquet")
    return df_modeling

def load_data(filename_base: str, folder: str = "data") -> tuple[pd.DataFrame, pd.DataFrame, dict]: """Load saved simulation data and parameters from files. Parameters ---------- filename_base : str Base filename used when saving files folder : str, optional Folder containing saved files, by default "data" Returns ------- tuple[pd.DataFrame, pd.DataFrame, dict] Contains: - DataFrame with modeling data - DataFrame with full data - Dict containing group and subject parameters """ df_modeling = pd.read_parquet(f"{folder}/{filename_base}_modeling.parquet") return df_modeling

In [5]:

workshop_data  = load_data(filename_base = "carney_workshop_2025",
                           folder = "scientific_workflow_hssm/data/")

workshop_data = load_data(filename_base = "carney_workshop_2025", folder = "scientific_workflow_hssm/data/")

Load Plotting Utilities¶

In [6]:

import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import inset_axes

def plot_rt_by_choice(df: pd.DataFrame,
                      categorical_column: str | None = None,
                      colors: dict[str, str] | dict[int, str] | None = None,
                      ax: plt.Axes | None = None):
    if categorical_column is None:
        ax.hist(df['rt'] * df['response'],
                bins = np.linspace(-5,5, 50), 
                # label=f'Condition {cond}', 
                histtype='step',
                density = True,
                color='tab:blue')
    else:
        for cond in df[categorical_column].unique():
            df_cond = df[df[categorical_column] == cond]
            ax.hist(df_cond['rt'] * df_cond['response'],
                    bins = np.linspace(-5,5, 50), 
                    label=f'Condition {cond}', 
                    histtype='step',
                    density = True,
                    color=colors[cond])
        ax.set_xlabel('RT * Choice')
        ax.set_ylabel('Density')
    return ax
        
def inset_bar_plot(df: pd.DataFrame, 
                   categorical_column: str,
                   response_options: list[int],
                   colors: dict[str, str] | dict[int, str] | None = None,
                   ax: plt.Axes | None = None):
    
    axins = inset_axes(ax, 
                       width="35%",
                       height="35%",
                       loc='upper left',
                       borderpad=2.75)
    bar_width = 0.55
    for j, resp in enumerate(response_options):
        for k, cond in enumerate(df[categorical_column].unique()):
            k_displace = -1 if k == 0 else 1
            df_cond = df[df[categorical_column] == cond]
            prop = (df_cond[df_cond.response == resp].shape[0] / len(df_cond))
            axins.bar((resp + ((bar_width / 2) * k_displace)), 
                        prop,
                        width=bar_width,
                        fill = False,
                        edgecolor=colors[cond],
                        label=f'Response {resp}')
    axins.set_xticks(response_options)
    axins.set_ylim(0, 1)
    axins.set_yticks([0.0, 0.5, 1])
    axins.set_title('choice proportion / option', fontsize=8)
    axins.tick_params(axis='both', which='major', labelsize=7)
    axins.set_xlabel('')
    axins.set_ylabel('')
    return ax

def inset_bar_plot_vertical(df: pd.DataFrame,
                            categorical_column: str,
                            response_options: list[int],
                            colors: dict[str, str] | dict[int, str] | None = None,
                            ax: plt.Axes | None = None):
    
    axins = inset_axes(ax,
                       width="35%",
                       height="35%",
                       loc='upper left',
                       borderpad=2.25)
    bar_width = 0.55
    for j, resp in enumerate(response_options):
        # k_displace_dict = {0:}
        for k, cond in enumerate(df[categorical_column].unique()):
            k_displace = -1 if k == 0 else 1
            df_cond = df[df[categorical_column] == cond]
            rt_mean = (df_cond[df_cond.response == resp]).rt.mean()
            axins.barh((resp + ((bar_width / 2) * k_displace)), 
                       rt_mean,
                       height=bar_width,
                       fill = False,
                       edgecolor=colors[cond],
                       label=f'Response {resp}')

    axins.set_yticks(response_options)
    axins.set_xticks([0.0, 1., 2.])
    axins.set_title('rt-mean by choice option', fontsize=8)
    axins.tick_params(axis='both', which='major', labelsize=7)
    axins.set_xlabel('')
    axins.set_ylabel('')
    return ax

def plot_rt_hists(df: pd.DataFrame,
                  by_participant: bool = True,
                  split_by_column: str | None = None,
                  inset_plot: str | None = "choice proportion",
                  cols: int = 5):
    if split_by_column is not None:
        colors = {cond: color for cond, color in zip(df[split_by_column].unique(), 
                            ['tab:blue', 'tab:orange', 'tab:green', 'tab:red', 'tab:purple'])}
    else:
        colors = None

    if by_participant:
        # Get unique participant IDs and costly_fail_conditions
        participants = df['participant_id'].unique()

        # Set up subplot grid (adjust cols as needed)
        rows = (len(participants) + cols - 1) // cols
        fig, axes = plt.subplots(rows, cols, 
                                 figsize=(cols*4, rows*3), 
                                 sharey=True, sharex=True)
        axes = axes.flatten()
        for i, pid in enumerate(participants):
            ax = axes[i]
            df_part = df[df['participant_id'] == pid]
            ax = plot_rt_by_choice(df_part,
                                   split_by_column,
                                   colors,
                                   ax)
            
            # Take care of inset plots
            if inset_plot == "choice_proportion":
                ax = inset_bar_plot(df_part, 
                                    split_by_column,
                                    df['response'].unique(),
                                    colors,
                                    ax)
            elif inset_plot == "rt_mean":
                ax = inset_bar_plot_vertical(df_part, 
                                             split_by_column,
                                             df['response'].unique(),
                                             colors,
                                             ax)
            if i == 0:
                ax.legend(title=split_by_column, loc='best', fontsize='small')

        # Hide unused axes
        for j in range(i+1, len(axes)):
            axes[j].set_visible(False)

        plt.tight_layout()
        plt.suptitle('RT, Split by Costly Fail Condition and Participant', y=1.02)
        plt.show()
    else:
        fig, ax = plt.subplots(1, 1, figsize=(4, 3))
        ax = plot_rt_by_choice(df,
                               split_by_column,
                               colors,
                               ax)

        # Take care of inset plots
        if inset_plot == "choice_proportion":
            ax = inset_bar_plot(df,
                                split_by_column,
                                df['response'].unique(),
                                colors,
                                ax)
        elif inset_plot == "rt_mean":
            ax = inset_bar_plot_vertical(df,
                                         split_by_column,
                                         df['response'].unique(),
                                         colors,
                                         ax)
        
        ax.legend(title=split_by_column, loc='best', fontsize='small')
        plt.tight_layout()
        plt.suptitle('RT by Trial, Split by Costly Fail Condition', y=1.02)
        plt.show()

import matplotlib.pyplot as plt from mpl_toolkits.axes_grid1.inset_locator import inset_axes def plot_rt_by_choice(df: pd.DataFrame, categorical_column: str | None = None, colors: dict[str, str] | dict[int, str] | None = None, ax: plt.Axes | None = None): if categorical_column is None: ax.hist(df['rt'] * df['response'], bins = np.linspace(-5,5, 50), # label=f'Condition {cond}', histtype='step', density = True, color='tab:blue') else: for cond in df[categorical_column].unique(): df_cond = df[df[categorical_column] == cond] ax.hist(df_cond['rt'] * df_cond['response'], bins = np.linspace(-5,5, 50), label=f'Condition {cond}', histtype='step', density = True, color=colors[cond]) ax.set_xlabel('RT * Choice') ax.set_ylabel('Density') return ax def inset_bar_plot(df: pd.DataFrame, categorical_column: str, response_options: list[int], colors: dict[str, str] | dict[int, str] | None = None, ax: plt.Axes | None = None): axins = inset_axes(ax, width="35%", height="35%", loc='upper left', borderpad=2.75) bar_width = 0.55 for j, resp in enumerate(response_options): for k, cond in enumerate(df[categorical_column].unique()): k_displace = -1 if k == 0 else 1 df_cond = df[df[categorical_column] == cond] prop = (df_cond[df_cond.response == resp].shape[0] / len(df_cond)) axins.bar((resp + ((bar_width / 2) * k_displace)), prop, width=bar_width, fill = False, edgecolor=colors[cond], label=f'Response {resp}') axins.set_xticks(response_options) axins.set_ylim(0, 1) axins.set_yticks([0.0, 0.5, 1]) axins.set_title('choice proportion / option', fontsize=8) axins.tick_params(axis='both', which='major', labelsize=7) axins.set_xlabel('') axins.set_ylabel('') return ax def inset_bar_plot_vertical(df: pd.DataFrame, categorical_column: str, response_options: list[int], colors: dict[str, str] | dict[int, str] | None = None, ax: plt.Axes | None = None): axins = inset_axes(ax, width="35%", height="35%", loc='upper left', borderpad=2.25) bar_width = 0.55 for j, resp in enumerate(response_options): # k_displace_dict = {0:} for k, cond in enumerate(df[categorical_column].unique()): k_displace = -1 if k == 0 else 1 df_cond = df[df[categorical_column] == cond] rt_mean = (df_cond[df_cond.response == resp]).rt.mean() axins.barh((resp + ((bar_width / 2) * k_displace)), rt_mean, height=bar_width, fill = False, edgecolor=colors[cond], label=f'Response {resp}') axins.set_yticks(response_options) axins.set_xticks([0.0, 1., 2.]) axins.set_title('rt-mean by choice option', fontsize=8) axins.tick_params(axis='both', which='major', labelsize=7) axins.set_xlabel('') axins.set_ylabel('') return ax def plot_rt_hists(df: pd.DataFrame, by_participant: bool = True, split_by_column: str | None = None, inset_plot: str | None = "choice proportion", cols: int = 5): if split_by_column is not None: colors = {cond: color for cond, color in zip(df[split_by_column].unique(), ['tab:blue', 'tab:orange', 'tab:green', 'tab:red', 'tab:purple'])} else: colors = None if by_participant: # Get unique participant IDs and costly_fail_conditions participants = df['participant_id'].unique() # Set up subplot grid (adjust cols as needed) rows = (len(participants) + cols - 1) // cols fig, axes = plt.subplots(rows, cols, figsize=(cols*4, rows*3), sharey=True, sharex=True) axes = axes.flatten() for i, pid in enumerate(participants): ax = axes[i] df_part = df[df['participant_id'] == pid] ax = plot_rt_by_choice(df_part, split_by_column, colors, ax) # Take care of inset plots if inset_plot == "choice_proportion": ax = inset_bar_plot(df_part, split_by_column, df['response'].unique(), colors, ax) elif inset_plot == "rt_mean": ax = inset_bar_plot_vertical(df_part, split_by_column, df['response'].unique(), colors, ax) if i == 0: ax.legend(title=split_by_column, loc='best', fontsize='small') # Hide unused axes for j in range(i+1, len(axes)): axes[j].set_visible(False) plt.tight_layout() plt.suptitle('RT, Split by Costly Fail Condition and Participant', y=1.02) plt.show() else: fig, ax = plt.subplots(1, 1, figsize=(4, 3)) ax = plot_rt_by_choice(df, split_by_column, colors, ax) # Take care of inset plots if inset_plot == "choice_proportion": ax = inset_bar_plot(df, split_by_column, df['response'].unique(), colors, ax) elif inset_plot == "rt_mean": ax = inset_bar_plot_vertical(df, split_by_column, df['response'].unique(), colors, ax) ax.legend(title=split_by_column, loc='best', fontsize='small') plt.tight_layout() plt.suptitle('RT by Trial, Split by Costly Fail Condition', y=1.02) plt.show()

Exploratory Data Analysis¶

Now that we are done preparing the setup, let's get to the meat of it! The picture above gives us a bit of an idea, where the dataset that we are going to work with below comes from (alert: the backstory may or may not be real).

20 subjects, performed 250 trials each of a basic Random dot motion task. The task seemingly had two important manipulations.

1. A costly fail condition, in which subjects get punished for mistakes.
2. A trial by trail manipulation of difficulty (in the Random dot motion task, this refers to degree of coherence with which the dots move in a particular direction)

Let's take a look at the actual dataframe.

In [7]:

workshop_data

workshop_data

Out[7]:

	response	rt	participant_id	trial	costly_fail_condition	continuous_difficulty	response_l1
0	1	0.556439	0	1	1	-0.277337	0
1	1	0.741682	0	2	0	-0.810919	1
2	1	0.461832	0	3	0	-0.673330	1
3	1	0.626154	0	4	0	0.755445	1
4	1	0.651677	0	5	1	0.136755	1
...	...	...	...	...	...	...	...
4995	1	1.039342	19	246	0	-0.612223	-1
4996	1	1.587827	19	247	0	0.732396	1
4997	1	0.668594	19	248	1	-0.175321	1
4998	1	1.616471	19	249	0	-0.630447	1
4999	1	1.051329	19	250	1	0.511197	1

5000 rows × 7 columns

Adding a few columns¶

As part of prep work for plotting etc. we will add a few columns here. These will be motivated later (close your eyes :)).

In [8]:

# Binary version of difficulty
workshop_data['bin_difficulty'] = workshop_data['continuous_difficulty'].apply(lambda x: 'high' if x > 0 else 'low')

# I want a a ordinal variable that is composed of 5 quantile levels of difficulty
workshop_data['quantile_difficulty'] = pd.qcut(workshop_data['continuous_difficulty'],
                                                             3, labels = ['-1', '0', '1'])

workshop_data['quantile_difficulty_binary'] = pd.qcut(workshop_data['continuous_difficulty'],
                                                             2, labels = ['-1', '1'])

# Slightly
workshop_data['response_l1_plotting'] = workshop_data['response_l1'].apply(lambda x: str(-1) if x == -1 else str(1))

# Binary version of difficulty workshop_data['bin_difficulty'] = workshop_data['continuous_difficulty'].apply(lambda x: 'high' if x > 0 else 'low') # I want a a ordinal variable that is composed of 5 quantile levels of difficulty workshop_data['quantile_difficulty'] = pd.qcut(workshop_data['continuous_difficulty'], 3, labels = ['-1', '0', '1']) workshop_data['quantile_difficulty_binary'] = pd.qcut(workshop_data['continuous_difficulty'], 2, labels = ['-1', '1']) # Slightly workshop_data['response_l1_plotting'] = workshop_data['response_l1'].apply(lambda x: str(-1) if x == -1 else str(1))

Most basic reaction time plot¶

In [9]:

plot_rt_hists(workshop_data, 
              by_participant = False, 
              split_by_column = None,
              inset_plot = None)

plot_rt_hists(workshop_data, by_participant = False, split_by_column = None, inset_plot = None)

/var/folders/gx/s43vynx550qbypcxm83fv56dzq4hgg/T/ipykernel_64548/900136031.py:166: UserWarning: No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
  ax.legend(title=split_by_column, loc='best', fontsize='small')

So far so good. Looking at the global reaction time pattern, it does seem commensurate with what we might expect out of basic Sequential Sampling Model (SSM). The basic DDM might be a good start here.

Basic Model: DDM¶

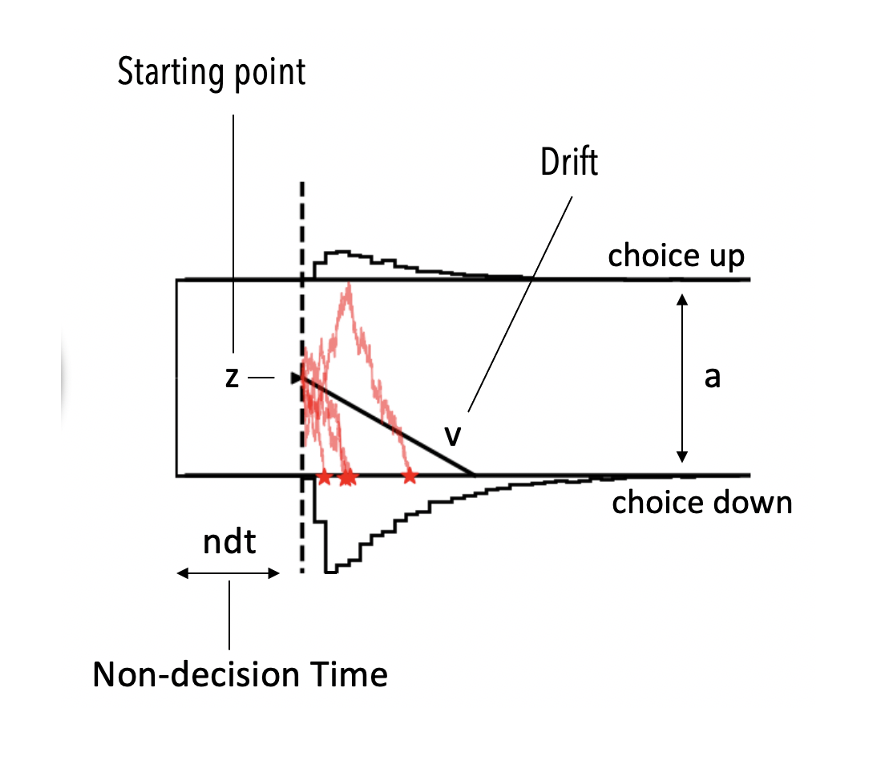
The picture above illustrates the basic Drift Diffusion Model. Note the parameters,

1. v the drift rate (how much evidence do I collect on average per unit of time)
2. a the boundary separation (how much evidence do I need to commit to a choice)
3. z how biased am I toward a particular choice a priori
4. ndt (we will simply call it t below), the delay between being exposed to a stimulus and starting the actual evidence accumulation process

In [10]:

BasicDDMModel = hssm.HSSM(data = workshop_data,
                          model = "ddm",
                          loglik_kind = "approx_differentiable",
                          global_formula = "y ~ 1",
                          noncentered = False,
                          )

BasicDDMModel = hssm.HSSM(data = workshop_data, model = "ddm", loglik_kind = "approx_differentiable", global_formula = "y ~ 1", noncentered = False, )

Model initialized successfully.

In [11]:

BasicDDMModel

BasicDDMModel

Out[11]:

Hierarchical Sequential Sampling Model
Model: ddm

Response variable: rt,response
Likelihood: approx_differentiable
Observations: 5000

Parameters:

v:
    Formula: v ~ 1
    Priors:
        v_Intercept ~ Normal(mu: 0.0, sigma: 0.25)
    Link: identity
    Explicit bounds: (-3.0, 3.0)

a:
    Formula: a ~ 1
    Priors:
        a_Intercept ~ Normal(mu: 1.4, sigma: 0.25)
    Link: identity
    Explicit bounds: (0.3, 2.5)

z:
    Formula: z ~ 1
    Priors:
        z_Intercept ~ Normal(mu: 0.5, sigma: 0.25)
    Link: identity
    Explicit bounds: (0.0, 1.0)

t:
    Formula: t ~ 1
    Priors:
        t_Intercept ~ Normal(mu: 1.0, sigma: 0.25)
    Link: identity
    Explicit bounds: (0.0, 2.0)


Lapse probability: 0.05
Lapse distribution: Uniform(lower: 0.0, upper: 20.0)

In [12]:

BasicDDMModel.graph()

BasicDDMModel.graph()

Out[12]:

In [13]:

try:
    # Load pre-computed traces
    BasicDDMModel.restore_traces(traces = "scientific_workflow_hssm/idata/basic_ddm/traces.nc")
except:
    # Sample posterior
    basic_ddm_idata = BasicDDMModel.sample(chains = 2,
                                            sampler = "nuts_numpyro",
                                            tune = 500,
                                            draws = 500,
                                        )

    # Sample posterior predictive
    BasicDDMModel.sample_posterior_predictive(draws = 200,
                                              safe_mode = True)

    # Save Model
    BasicDDMModel.save_model(model_name = "basic_ddm",
                             allow_absolute_base_path = True,
                             base_path = "scientific_workflow_hssm/idata/",
                             save_idata_only = True)

try: # Load pre-computed traces BasicDDMModel.restore_traces(traces = "scientific_workflow_hssm/idata/basic_ddm/traces.nc") except: # Sample posterior basic_ddm_idata = BasicDDMModel.sample(chains = 2, sampler = "nuts_numpyro", tune = 500, draws = 500, ) # Sample posterior predictive BasicDDMModel.sample_posterior_predictive(draws = 200, safe_mode = True) # Save Model BasicDDMModel.save_model(model_name = "basic_ddm", allow_absolute_base_path = True, base_path = "scientific_workflow_hssm/idata/", save_idata_only = True)

In [14]:

BasicDDMModel.traces

BasicDDMModel.traces

Out[14]:

arviz.InferenceData

• posterior

  <xarray.Dataset> Size: 36kB
  Dimensions:      (chain: 2, draw: 500)
  Coordinates:
    * chain        (chain) int64 16B 0 1
    * draw         (draw) int64 4kB 0 1 2 3 4 5 6 ... 493 494 495 496 497 498 499
  Data variables:
      t_Intercept  (chain, draw) float64 8kB ...
      z_Intercept  (chain, draw) float64 8kB ...
      a_Intercept  (chain, draw) float64 8kB ...
      v_Intercept  (chain, draw) float64 8kB ...
  Attributes:
      created_at:                  2025-07-11T17:29:22.668745+00:00
      arviz_version:               0.21.0
      inference_library:           numpyro
      inference_library_version:   0.17.0
      sampling_time:               95.06823
      tuning_steps:                500
      modeling_interface:          bambi
      modeling_interface_version:  0.15.0

  xarray.Dataset

  • Dimensions:
    • chain: 2
    • draw: 500
  • Coordinates: (2)
    • chain
      (chain)
      int64
      0 1

      array([0, 1])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 495 496 497 498 499

      array([  0,   1,   2, ..., 497, 498, 499], shape=(500,))

  • Data variables: (4)
    • t_Intercept
      (chain, draw)
      float64
      ...

      [1000 values with dtype=float64]

    • z_Intercept
      (chain, draw)
      float64
      ...

      [1000 values with dtype=float64]

    • a_Intercept
      (chain, draw)
      float64
      ...

      [1000 values with dtype=float64]

    • v_Intercept
      (chain, draw)
      float64
      ...

      [1000 values with dtype=float64]

  • Indexes: (2)
    • chain
      PandasIndex

      PandasIndex(Index([0, 1], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
             ...
             490, 491, 492, 493, 494, 495, 496, 497, 498, 499],
            dtype='int64', name='draw', length=500))

  • Attributes: (8)

    created_at :

    2025-07-11T17:29:22.668745+00:00

    arviz_version :

    0.21.0

    inference_library :

    numpyro

    inference_library_version :

    0.17.0

    sampling_time :

    95.06823

    tuning_steps :

    500

    modeling_interface :

    bambi

    modeling_interface_version :

    0.15.0

  
  
• posterior_predictive

  <xarray.Dataset> Size: 32MB
  Dimensions:          (chain: 2, draw: 200, __obs__: 5000, rt,response_dim: 2)
  Coordinates:
    * chain            (chain) int64 16B 0 1
    * draw             (draw) int64 2kB 0 1 2 3 4 5 6 ... 194 195 196 197 198 199
    * __obs__          (__obs__) int64 40kB 0 1 2 3 4 ... 4995 4996 4997 4998 4999
    * rt,response_dim  (rt,response_dim) int64 16B 0 1
  Data variables:
      rt,response      (chain, draw, __obs__, rt,response_dim) float64 32MB ...
  Attributes:
      modeling_interface:          bambi
      modeling_interface_version:  0.15.0

  xarray.Dataset

  • Dimensions:
    • chain: 2
    • draw: 200
    • __obs__: 5000
    • rt,response_dim: 2
  • Coordinates: (4)
    • chain
      (chain)
      int64
      0 1

      array([0, 1])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 195 196 197 198 199

      array([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,  10,  11,  12,  13,
              14,  15,  16,  17,  18,  19,  20,  21,  22,  23,  24,  25,  26,  27,
              28,  29,  30,  31,  32,  33,  34,  35,  36,  37,  38,  39,  40,  41,
              42,  43,  44,  45,  46,  47,  48,  49,  50,  51,  52,  53,  54,  55,
              56,  57,  58,  59,  60,  61,  62,  63,  64,  65,  66,  67,  68,  69,
              70,  71,  72,  73,  74,  75,  76,  77,  78,  79,  80,  81,  82,  83,
              84,  85,  86,  87,  88,  89,  90,  91,  92,  93,  94,  95,  96,  97,
              98,  99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111,
             112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125,
             126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139,
             140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153,
             154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167,
             168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181,
             182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195,
             196, 197, 198, 199])

    • __obs__
      (__obs__)
      int64
      0 1 2 3 4 ... 4996 4997 4998 4999

      array([   0,    1,    2, ..., 4997, 4998, 4999], shape=(5000,))

    • rt,response_dim
      (rt,response_dim)
      int64
      0 1

      array([0, 1])

  • Data variables: (1)
    • rt,response
      (chain, draw, __obs__, rt,response_dim)
      float64
      ...

      [4000000 values with dtype=float64]

  • Indexes: (4)
    • chain
      PandasIndex

      PandasIndex(Index([0, 1], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
             ...
             190, 191, 192, 193, 194, 195, 196, 197, 198, 199],
            dtype='int64', name='draw', length=200))

    • __obs__
      PandasIndex

      PandasIndex(Index([   0,    1,    2,    3,    4,    5,    6,    7,    8,    9,
             ...
             4990, 4991, 4992, 4993, 4994, 4995, 4996, 4997, 4998, 4999],
            dtype='int64', name='__obs__', length=5000))

    • rt,response_dim
      PandasIndex

      PandasIndex(Index([0, 1], dtype='int64', name='rt,response_dim'))

  • Attributes: (2)

    modeling_interface :

    bambi

    modeling_interface_version :

    0.15.0

  
  
• log_likelihood

  <xarray.Dataset> Size: 40MB
  Dimensions:      (chain: 2, draw: 500, __obs__: 5000)
  Coordinates:
    * chain        (chain) int64 16B 0 1
    * draw         (draw) int64 4kB 0 1 2 3 4 5 6 ... 493 494 495 496 497 498 499
    * __obs__      (__obs__) int64 40kB 0 1 2 3 4 5 ... 4995 4996 4997 4998 4999
  Data variables:
      rt,response  (chain, draw, __obs__) float64 40MB ...
  Attributes:
      modeling_interface:          bambi
      modeling_interface_version:  0.15.0

  xarray.Dataset

  • Dimensions:
    • chain: 2
    • draw: 500
    • __obs__: 5000
  • Coordinates: (3)
    • chain
      (chain)
      int64
      0 1

      array([0, 1])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 495 496 497 498 499

      array([  0,   1,   2, ..., 497, 498, 499], shape=(500,))

    • __obs__
      (__obs__)
      int64
      0 1 2 3 4 ... 4996 4997 4998 4999

      array([   0,    1,    2, ..., 4997, 4998, 4999], shape=(5000,))

  • Data variables: (1)
    • rt,response
      (chain, draw, __obs__)
      float64
      ...

      [5000000 values with dtype=float64]

  • Indexes: (3)
    • chain
      PandasIndex

      PandasIndex(Index([0, 1], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
             ...
             490, 491, 492, 493, 494, 495, 496, 497, 498, 499],
            dtype='int64', name='draw', length=500))

    • __obs__
      PandasIndex

      PandasIndex(Index([   0,    1,    2,    3,    4,    5,    6,    7,    8,    9,
             ...
             4990, 4991, 4992, 4993, 4994, 4995, 4996, 4997, 4998, 4999],
            dtype='int64', name='__obs__', length=5000))

  • Attributes: (2)

    modeling_interface :

    bambi

    modeling_interface_version :

    0.15.0

  
  
• sample_stats

  <xarray.Dataset> Size: 53kB
  Dimensions:          (chain: 2, draw: 500)
  Coordinates:
    * chain            (chain) int64 16B 0 1
    * draw             (draw) int64 4kB 0 1 2 3 4 5 6 ... 494 495 496 497 498 499
  Data variables:
      acceptance_rate  (chain, draw) float64 8kB ...
      step_size        (chain, draw) float64 8kB ...
      diverging        (chain, draw) bool 1kB ...
      energy           (chain, draw) float64 8kB ...
      n_steps          (chain, draw) int64 8kB ...
      tree_depth       (chain, draw) int64 8kB ...
      lp               (chain, draw) float64 8kB ...
  Attributes:
      created_at:                  2025-07-11T17:29:22.675898+00:00
      arviz_version:               0.21.0
      modeling_interface:          bambi
      modeling_interface_version:  0.15.0

  xarray.Dataset

  • Dimensions:
    • chain: 2
    • draw: 500
  • Coordinates: (2)
    • chain
      (chain)
      int64
      0 1

      array([0, 1])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 495 496 497 498 499

      array([  0,   1,   2, ..., 497, 498, 499], shape=(500,))

  • Data variables: (7)
    • acceptance_rate
      (chain, draw)
      float64
      ...

      [1000 values with dtype=float64]

    • step_size
      (chain, draw)
      float64
      ...

      [1000 values with dtype=float64]

    • diverging
      (chain, draw)
      bool
      ...

      [1000 values with dtype=bool]

    • energy
      (chain, draw)
      float64
      ...

      [1000 values with dtype=float64]

    • n_steps
      (chain, draw)
      int64
      ...

      [1000 values with dtype=int64]

    • tree_depth
      (chain, draw)
      int64
      ...

      [1000 values with dtype=int64]

    • lp
      (chain, draw)
      float64
      ...

      [1000 values with dtype=float64]

  • Indexes: (2)
    • chain
      PandasIndex

      PandasIndex(Index([0, 1], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
             ...
             490, 491, 492, 493, 494, 495, 496, 497, 498, 499],
            dtype='int64', name='draw', length=500))

  • Attributes: (4)

    created_at :

    2025-07-11T17:29:22.675898+00:00

    arviz_version :

    0.21.0

    modeling_interface :

    bambi

    modeling_interface_version :

    0.15.0

  
  
• observed_data

  <xarray.Dataset> Size: 120kB
  Dimensions:                  (__obs__: 5000, rt,response_extra_dim_0: 2)
  Coordinates:
    * __obs__                  (__obs__) int64 40kB 0 1 2 3 ... 4997 4998 4999
    * rt,response_extra_dim_0  (rt,response_extra_dim_0) int64 16B 0 1
  Data variables:
      rt,response              (__obs__, rt,response_extra_dim_0) float64 80kB ...
  Attributes:
      created_at:                  2025-07-11T17:29:22.676800+00:00
      arviz_version:               0.21.0
      inference_library:           numpyro
      inference_library_version:   0.17.0
      sampling_time:               95.06823
      tuning_steps:                500
      modeling_interface:          bambi
      modeling_interface_version:  0.15.0

  xarray.Dataset

  • Dimensions:
    • __obs__: 5000
    • rt,response_extra_dim_0: 2
  • Coordinates: (2)
    • __obs__
      (__obs__)
      int64
      0 1 2 3 4 ... 4996 4997 4998 4999

      array([   0,    1,    2, ..., 4997, 4998, 4999], shape=(5000,))

    • rt,response_extra_dim_0
      (rt,response_extra_dim_0)
      int64
      0 1

      array([0, 1])

  • Data variables: (1)
    • rt,response
      (__obs__, rt,response_extra_dim_0)
      float64
      ...

      [10000 values with dtype=float64]

  • Indexes: (2)
    • __obs__
      PandasIndex

      PandasIndex(Index([   0,    1,    2,    3,    4,    5,    6,    7,    8,    9,
             ...
             4990, 4991, 4992, 4993, 4994, 4995, 4996, 4997, 4998, 4999],
            dtype='int64', name='__obs__', length=5000))

    • rt,response_extra_dim_0
      PandasIndex

      PandasIndex(Index([0, 1], dtype='int64', name='rt,response_extra_dim_0'))

  • Attributes: (8)

    created_at :

    2025-07-11T17:29:22.676800+00:00

    arviz_version :

    0.21.0

    inference_library :

    numpyro

    inference_library_version :

    0.17.0

    sampling_time :

    95.06823

    tuning_steps :

    500

    modeling_interface :

    bambi

    modeling_interface_version :

    0.15.0

  
  

In [15]:

az.summary(BasicDDMModel.traces)

az.summary(BasicDDMModel.traces)

Out[15]:

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
t_Intercept	0.328	0.005	0.317	0.338	0.000	0.000	576.0	573.0	1.0
z_Intercept	0.466	0.007	0.453	0.478	0.000	0.000	529.0	496.0	1.0
a_Intercept	1.017	0.009	1.000	1.033	0.000	0.000	583.0	610.0	1.0
v_Intercept	0.943	0.023	0.900	0.985	0.001	0.001	536.0	526.0	1.0

In [16]:

az.plot_trace(BasicDDMModel.traces)
plt.tight_layout()

az.plot_trace(BasicDDMModel.traces) plt.tight_layout()

In [17]:

az.plot_forest(BasicDDMModel.traces)
plt.tight_layout()

az.plot_forest(BasicDDMModel.traces) plt.tight_layout()

In [18]:

az.plot_pair(BasicDDMModel.traces,
             kind="kde",
             marginals=True)

az.plot_pair(BasicDDMModel.traces, kind="kde", marginals=True)

Out[18]:

array([[<Axes: ylabel='t_Intercept'>, <Axes: >, <Axes: >, <Axes: >],
       [<Axes: ylabel='z_Intercept'>, <Axes: >, <Axes: >, <Axes: >],
       [<Axes: ylabel='a_Intercept'>, <Axes: >, <Axes: >, <Axes: >],
       [<Axes: xlabel='t_Intercept', ylabel='v_Intercept'>,
        <Axes: xlabel='z_Intercept'>, <Axes: xlabel='a_Intercept'>,
        <Axes: xlabel='v_Intercept'>]], dtype=object)

In [19]:

ax = hssm.plotting.plot_model_cartoon(
    BasicDDMModel,
    n_samples=10,
    bins=20,
    plot_pp_mean=True,
    plot_pp_samples=False,
    n_trajectories=2,  # extra arguments for the underlying plot_model_cartoon() function
);

ax = hssm.plotting.plot_model_cartoon( BasicDDMModel, n_samples=10, bins=20, plot_pp_mean=True, plot_pp_samples=False, n_trajectories=2, # extra arguments for the underlying plot_model_cartoon() function );

No posterior predictive samples found. Generating posterior predictive samples using the provided InferenceData object and the original data. This will modify the provided InferenceData object, or if not provided, the traces object stored inside the model.

Output()

Output()

Output()

Output()

In [20]:

ax = hssm.plotting.plot_quantile_probability(BasicDDMModel, 
                                             cond="quantile_difficulty",
                                             )
ax.set_ylim(0, 3);
# ax.set_xlim(-0.1, 1.1);

ax = hssm.plotting.plot_quantile_probability(BasicDDMModel, cond="quantile_difficulty", ) ax.set_ylim(0, 3); # ax.set_xlim(-0.1, 1.1);

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/src/hssm/plotting/utils.py:327: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df.groupby(["observed", "chain", "draw", cond, "is_correct"])["rt"]
/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/src/hssm/plotting/utils.py:334: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df.groupby(["observed", "chain", "draw", cond])["is_correct"]

In [21]:

ax = hssm.plotting.plot_quantile_probability(BasicDDMModel, 
                                             cond="costly_fail_condition",
                                             )
ax.set_ylim(0, 3);

ax = hssm.plotting.plot_quantile_probability(BasicDDMModel, cond="costly_fail_condition", ) ax.set_ylim(0, 3);

In [22]:

ax = hssm.plotting.plot_quantile_probability(BasicDDMModel, 
                                             cond="response_l1_plotting",
                                             )
ax.set_ylim(0, 3);

ax = hssm.plotting.plot_quantile_probability(BasicDDMModel, cond="response_l1_plotting", ) ax.set_ylim(0, 3);

In [23]:

# Posterior predictive
BasicDDMModel.plot_posterior_predictive(step = True, 
                                        col = 'participant_id',
                                        col_wrap = 5,
                                        bins = np.linspace(-5,5, 50))

# Posterior predictive BasicDDMModel.plot_posterior_predictive(step = True, col = 'participant_id', col_wrap = 5, bins = np.linspace(-5,5, 50))

Out[23]:

<seaborn.axisgrid.FacetGrid at 0x2ba7a3110>

Taking stock¶

We can observe a few patterns here.

• First, cleary the reaction time distributions are not the same for every subject, we need to account for that.
• Second, I does seem like the tail of the reaction time distribution is more graceful in for our predictions than it is in the original subject data. (This was less clear when looking only at the global pattern...)

We will now adjust our model to tackle these patterns one by one. Let's begin by specializing our parameters by subject.

In Bayesian Inference we approach this by introducing a Hierarchy, we assume that subject level parameters derive from a common group distribution.

Inference then proceeds over the parameters of this group distribution, as well as the subject wise parameters.

Hierarchies serve as a form of regularization of our parameter estimates, the group distribution allows us to share information between the single subject parameters estimates.

You don't have to use a hierarchy, we could introduce a subject wise parameterization e.g. by simply treating participant_id as a categorical variable / collection of dummy variables without using any notion of a group distribution (and you are welcome to try this).

DDM Hierarchical¶

Moving on to our first hierarchical model. As a first step, we will use our global_formula argument to (1|participant_id), which is equivalent to 1 + (1|participant_id), (use 0 + (1|participant_id) is you explicitly don't want to create an intercept).

This will make all parameters of our model hierarchical.

In [24]:

DDMHierModel = hssm.HSSM(data = workshop_data,
                         model = "ddm",
                         loglik_kind = "approx_differentiable",
                         global_formula = "y ~ (1|participant_id)", # New
                         noncentered = False,
                        )

DDMHierModel = hssm.HSSM(data = workshop_data, model = "ddm", loglik_kind = "approx_differentiable", global_formula = "y ~ (1|participant_id)", # New noncentered = False, )

Model initialized successfully.

In [25]:

try:
    # Load pre-computed traces
    DDMHierModel.restore_traces(traces = "scientific_workflow_hssm/idata/ddm_hier/traces.nc")
except:
    # Sample posterior
    ddm_hier_idata = DDMHierModel.sample(chains = 2,
                                             sampler = "nuts_numpyro",
                                             tune = 500,
                                             draws = 500,
                                            )

    # Sample posterior predictive
    DDMHierModel.sample_posterior_predictive(draws = 200,
                                             safe_mode = True)

    # Save Model
    DDMHierModel.save_model(model_name = "ddm_hier",
                            allow_absolute_base_path = True,
                            base_path = "scientific_workflow_hssm/idata/",
                            save_idata_only = True)

try: # Load pre-computed traces DDMHierModel.restore_traces(traces = "scientific_workflow_hssm/idata/ddm_hier/traces.nc") except: # Sample posterior ddm_hier_idata = DDMHierModel.sample(chains = 2, sampler = "nuts_numpyro", tune = 500, draws = 500, ) # Sample posterior predictive DDMHierModel.sample_posterior_predictive(draws = 200, safe_mode = True) # Save Model DDMHierModel.save_model(model_name = "ddm_hier", allow_absolute_base_path = True, base_path = "scientific_workflow_hssm/idata/", save_idata_only = True)

In [26]:

DDMHierModel.graph()

DDMHierModel.graph()

Out[26]:

In [27]:

az.plot_trace(DDMHierModel.traces)
plt.tight_layout()

az.plot_trace(DDMHierModel.traces) plt.tight_layout()

In [28]:

ax = hssm.plotting.plot_model_cartoon(
    DDMHierModel,
    col = "participant_id",
    col_wrap = 5,
    n_samples=100,
    bin_size=0.2,
    plot_pp_mean=True,
    # color_pp_mean = "red",
    # color_pp = "black",
    plot_pp_samples=False,
    n_trajectories=2,  # extra arguments for the underlying plot_model_cartoon() function
);

ax = hssm.plotting.plot_model_cartoon( DDMHierModel, col = "participant_id", col_wrap = 5, n_samples=100, bin_size=0.2, plot_pp_mean=True, # color_pp_mean = "red", # color_pp = "black", plot_pp_samples=False, n_trajectories=2, # extra arguments for the underlying plot_model_cartoon() function );

No posterior predictive samples found. Generating posterior predictive samples using the provided InferenceData object and the original data. This will modify the provided InferenceData object, or if not provided, the traces object stored inside the model.

Output()

Output()

Output()

Output()

Comparing Parameter Loadings¶

In [29]:

az.summary(DDMHierModel.traces,
           filter_vars = "like",
           var_names = ["~participant_id"]).sort_index()

az.summary(DDMHierModel.traces, filter_vars = "like", var_names = ["~participant_id"]).sort_index()

Out[29]:

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
a_Intercept	1.041	0.019	1.005	1.078	0.001	0.001	311.0	398.0	1.01
t_Intercept	0.375	0.021	0.337	0.414	0.002	0.002	89.0	121.0	1.01
v_Intercept	0.948	0.110	0.734	1.146	0.010	0.006	121.0	205.0	1.01
z_Intercept	0.455	0.016	0.424	0.485	0.001	0.001	190.0	259.0	1.01

In [30]:

az.summary(BasicDDMModel.traces).sort_index()

az.summary(BasicDDMModel.traces).sort_index()

Out[30]:

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
a_Intercept	1.017	0.009	1.000	1.033	0.000	0.000	583.0	610.0	1.0
t_Intercept	0.328	0.005	0.317	0.338	0.000	0.000	576.0	573.0	1.0
v_Intercept	0.943	0.023	0.900	0.985	0.001	0.001	536.0	526.0	1.0
z_Intercept	0.466	0.007	0.453	0.478	0.000	0.000	529.0	496.0	1.0

The mean parameters of our models are de facto quite similar. Allowing subject wise variation however dramatically improved our fit to the data!

Quantitative Model Comparison¶

In [31]:

az.compare(
    {"DDM": BasicDDMModel.traces, 
     "DDM Hierarchical": DDMHierModel.traces}
)

az.compare( {"DDM": BasicDDMModel.traces, "DDM Hierarchical": DDMHierModel.traces} )

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/stats/stats.py:797: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.67 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

Out[31]:

	rank	elpd_loo	p_loo	elpd_diff	weight	se	dse	warning	scale
DDM Hierarchical	0	-4954.407753	74.496783	0.000000	0.999617	76.438410	0.000000	True	log
DDM	1	-5645.531361	4.771162	691.123609	0.000383	74.728599	32.604471	False	log

Comparing predictions¶

In [32]:

# Posterior predictive
DDMHierModel.plot_posterior_predictive(step = True, 
                                       col_wrap = 5,
                                       bins = np.linspace(-5,5, 50));

# Posterior predictive DDMHierModel.plot_posterior_predictive(step = True, col_wrap = 5, bins = np.linspace(-5,5, 50));

In [33]:

# Posterior predictive
BasicDDMModel.plot_posterior_predictive(step = True, 
                                        col_wrap = 5,
                                        bins = np.linspace(-5,5, 50));

# Posterior predictive BasicDDMModel.plot_posterior_predictive(step = True, col_wrap = 5, bins = np.linspace(-5,5, 50));

In [34]:

# Posterior predictive
DDMHierModel.plot_posterior_predictive(step = True, 
                                       col = 'participant_id',
                                       col_wrap = 5,
                                       bins = np.linspace(-5,5, 50))

# Posterior predictive DDMHierModel.plot_posterior_predictive(step = True, col = 'participant_id', col_wrap = 5, bins = np.linspace(-5,5, 50))

Out[34]:

<seaborn.axisgrid.FacetGrid at 0x2d129f850>

Taking Stock¶

Let's take stock again of any obvious pontential for improving our model here. We are now capturing the data much better subject by subject, however looking closely,

it seems like the tail behavior of the observed and the predicted data is somewhat different, for a few subjects.

The particularly suspicious subjest, are:

• participant_id = 1
• participant_id = 14
• participant_id = 15
• participant_id = 17

It seems that for these (and there are others) participants, the model predicted data has a wider tail than what we actually observe in our dataset.

This will motivate a change in the Sequential Sampling Model that we apply.

Angle Model Hierarchical¶

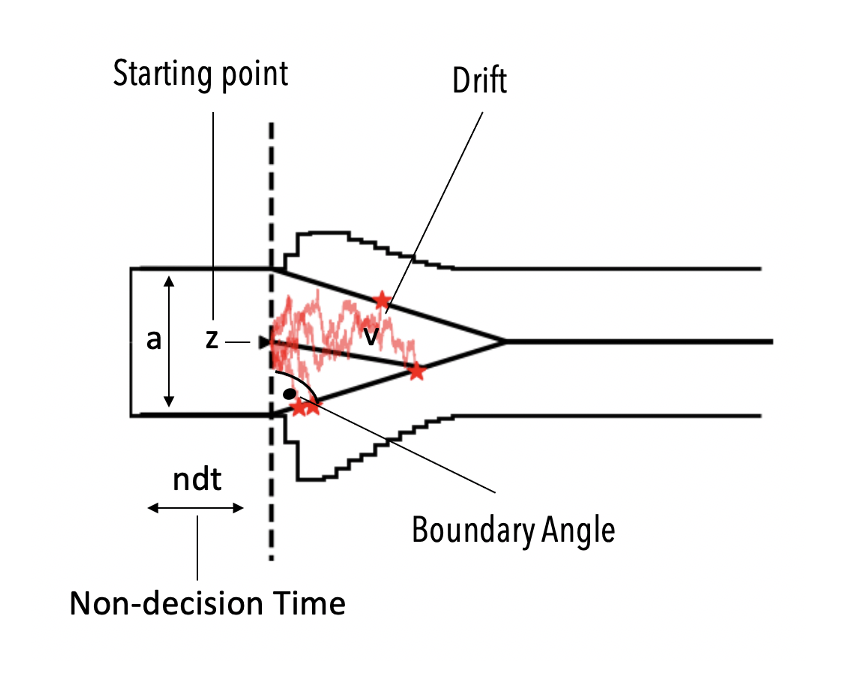
Given what we concluded about the tail behavior of the observed RTs, we will adjust our SSM, to allow for linear collapsing bounds. HSSM ships with a such a model, and we can apply it to our data simple by changing the model argument. The corresponding model is called angle model in our lingo, and is illustrated below conceptually.

In [35]:

AngleHierModel = hssm.HSSM(data = workshop_data,
                           model = "angle",
                           loglik_kind = "approx_differentiable",
                           global_formula = "y ~ (1|participant_id)",
                           noncentered = False,
                          )

AngleHierModel = hssm.HSSM(data = workshop_data, model = "angle", loglik_kind = "approx_differentiable", global_formula = "y ~ (1|participant_id)", noncentered = False, )

Model initialized successfully.

In [36]:

AngleHierModel.graph()

AngleHierModel.graph()

Out[36]:

In [37]:

try:
    # Load pre-computed traces
    AngleHierModel.restore_traces(traces = "scientific_workflow_hssm/idata/angle_hier/traces.nc")
except:
    # Sample posterior
    angle_hier_idata = AngleHierModel.sample(chains = 2,
                                             sampler = "nuts_numpyro",
                                             tune = 500,
                                             draws = 500,
                                            )

    # Sample posterior predictive
    AngleHierModel.sample_posterior_predictive(draws = 200,
                                               safe_mode = True)

    # Save Model
    AngleHierModel.save_model(model_name = "angle_hier",
                              allow_absolute_base_path = True,
                              base_path = "scientific_workflow_hssm/idata/",
                              save_idata_only = True)

try: # Load pre-computed traces AngleHierModel.restore_traces(traces = "scientific_workflow_hssm/idata/angle_hier/traces.nc") except: # Sample posterior angle_hier_idata = AngleHierModel.sample(chains = 2, sampler = "nuts_numpyro", tune = 500, draws = 500, ) # Sample posterior predictive AngleHierModel.sample_posterior_predictive(draws = 200, safe_mode = True) # Save Model AngleHierModel.save_model(model_name = "angle_hier", allow_absolute_base_path = True, base_path = "scientific_workflow_hssm/idata/", save_idata_only = True)

In [38]:

ax = hssm.plotting.plot_model_cartoon(
    AngleHierModel,
    col = 'participant_id',
    col_wrap = 5,
    n_samples=10,
    bin_size=0.2,
    plot_pp_mean=True,
    plot_pp_samples=False,
    n_trajectories=2,  # extra arguments for the underlying plot_model_cartoon() function
);

ax = hssm.plotting.plot_model_cartoon( AngleHierModel, col = 'participant_id', col_wrap = 5, n_samples=10, bin_size=0.2, plot_pp_mean=True, plot_pp_samples=False, n_trajectories=2, # extra arguments for the underlying plot_model_cartoon() function );

No posterior predictive samples found. Generating posterior predictive samples using the provided InferenceData object and the original data. This will modify the provided InferenceData object, or if not provided, the traces object stored inside the model.

Output()

Output()

Output()

Output()

Output()

In [ ]:

We can up it one notch and include the parameter uncertainty in the model_cartoon_plot(). This helps us assess how certain we are about the setting of the boundary collapse here. Let's see what that looks like!

In [39]:

ax = hssm.plotting.plot_model_cartoon(
    AngleHierModel,
    col = 'participant_id',
    col_wrap = 5,
    n_samples=50,
    bin_size=0.2,
    plot_pp_mean=True,
    plot_pp_samples=True,
    n_trajectories=2,  # extra arguments for the underlying plot_model_cartoon() function
);

ax = hssm.plotting.plot_model_cartoon( AngleHierModel, col = 'participant_id', col_wrap = 5, n_samples=50, bin_size=0.2, plot_pp_mean=True, plot_pp_samples=True, n_trajectories=2, # extra arguments for the underlying plot_model_cartoon() function );

No posterior predictive samples found. Generating posterior predictive samples using the provided InferenceData object and the original data. This will modify the provided InferenceData object, or if not provided, the traces object stored inside the model.

Output()

Output()

Output()

Output()

Output()

Output()

Output()

Output()

Output()

Output()

Angle (theta) parameter Bayesian t-test¶

In [40]:

az.plot_posterior(AngleHierModel.traces,
                  var_names = ["theta_Intercept"],
                  ref_val = 0,
                  kind = "hist",
                  ref_val_color = "red",
                  histtype = "step")

az.plot_posterior(AngleHierModel.traces, var_names = ["theta_Intercept"], ref_val = 0, kind = "hist", ref_val_color = "red", histtype = "step")

Out[40]:

<Axes: title={'center': 'theta_Intercept'}>

In [41]:

# Posterior predictive
AngleHierModel.plot_posterior_predictive(step = True, 
                                         col_wrap = 5,
                                         bins = np.linspace(-5,5, 50))

# Posterior predictive AngleHierModel.plot_posterior_predictive(step = True, col_wrap = 5, bins = np.linspace(-5,5, 50))

Out[41]:

<Axes: title={'center': 'Posterior Predictive Distribution'}, xlabel='Response Time', ylabel='Density'>

In [42]:

# Posterior predictive
AngleHierModel.plot_posterior_predictive(step = True, 
                                        col = 'participant_id',
                                        col_wrap = 5,
                                        bins = np.linspace(-5,5, 50))

# Posterior predictive AngleHierModel.plot_posterior_predictive(step = True, col = 'participant_id', col_wrap = 5, bins = np.linspace(-5,5, 50))

Out[42]:

<seaborn.axisgrid.FacetGrid at 0x3124ee5d0>

Visually it seems like we did improve the fit (even though the difference in visual improvement is much less than what we had witnessed introducing the hierarchy in the first place).

Let us corroborate the visual intuition via formal model comparison.

Quantitative Model Comparison¶

In [43]:

az.compare(
    {"DDM": BasicDDMModel.traces,
     "DDM Hierarchical": DDMHierModel.traces,
     "Angle Hierarchical": AngleHierModel.traces}
)

az.compare( {"DDM": BasicDDMModel.traces, "DDM Hierarchical": DDMHierModel.traces, "Angle Hierarchical": AngleHierModel.traces} )

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/stats/stats.py:797: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.67 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

Out[43]:

	rank	elpd_loo	p_loo	elpd_diff	weight	se	dse	warning	scale
Angle Hierarchical	0	-4736.150740	78.295641	0.000000	1.000000e+00	72.823473	0.000000	False	log
DDM Hierarchical	1	-4954.407753	74.496783	218.257012	1.547572e-07	76.438410	16.444052	True	log
DDM	2	-5645.531361	4.771162	909.380621	0.000000e+00	74.728599	36.362620	False	log

Good, introducing the angle model seemed to have helped us quite a bit, even though, as intuited by the simple visual inspection, the improvement in elpd_loo is not as the improvement in going from a simple model toward a hierarchical model (even though the actual SSM was misspecified).

So what next? On the surface, it looks like we have a model that fits our data quite well.

Let's take another look at our data to identify more patterns that we may not capture with out current efforts.

Further EDA¶

Maybe it is time to look more directly at the effects of our experiment manipulations.

Below are a few graphs to understand what might be happening.

In [44]:

# Posterior predictive
AngleHierModel.plot_posterior_predictive(step = True, 
                                         col = 'costly_fail_condition',
                                         bins = np.linspace(-5,5, 50))
plt.tight_layout()

# Posterior predictive AngleHierModel.plot_posterior_predictive(step = True, col = 'costly_fail_condition', bins = np.linspace(-5,5, 50)) plt.tight_layout()

In [45]:

ax = hssm.plotting.plot_quantile_probability(AngleHierModel, 
                                             cond="costly_fail_condition",
                                             )
ax.set_ylim(0, 3);

ax = hssm.plotting.plot_quantile_probability(AngleHierModel, cond="costly_fail_condition", ) ax.set_ylim(0, 3);

In [46]:

plot_rt_hists(workshop_data,
              by_participant = True,
              split_by_column = "costly_fail_condition",
              inset_plot =  "choice_proportion")

plot_rt_hists(workshop_data, by_participant = True, split_by_column = "costly_fail_condition", inset_plot = "choice_proportion")

/var/folders/gx/s43vynx550qbypcxm83fv56dzq4hgg/T/ipykernel_64548/900136031.py:142: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
  plt.tight_layout()

In [47]:

plot_rt_hists(workshop_data,
              by_participant = True,
              split_by_column = "costly_fail_condition",
              inset_plot =  "rt_mean")

plot_rt_hists(workshop_data, by_participant = True, split_by_column = "costly_fail_condition", inset_plot = "rt_mean")

/var/folders/gx/s43vynx550qbypcxm83fv56dzq4hgg/T/ipykernel_64548/900136031.py:142: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
  plt.tight_layout()

We can identify two patterns.

1. On average in the costly_fail_condition participants seem to make slightly fewer mistakes
2. On average in the costly_fail_condition participants seem to take a little longer for their choices!

This meshes with how we expect the incentives to act. Participants should be slightly more cautious to get it right, if mistakes are costly!

In the contect of SSMs, this is usually mapped on to the decision threshold (parameter a), so maybe we should try to incorporate the costly_fail_condition in the regression function for that parameter in our model.

Addressing costly fail condition¶

To include parameter specific regressions, we can rely on the include argument in HSSM. Let's illustrate this.

In [48]:

AngleHierModelV2 = hssm.HSSM(data = workshop_data,
                             model = "angle",
                             loglik_kind = "approx_differentiable",
                             global_formula = "y ~ (1|participant_id)",
                             include = [{"name": "a",
                                         "formula": "a ~ (1 + C(costly_fail_condition)|participant_id)"}],
                             noncentered = False,
                            )

AngleHierModelV2 = hssm.HSSM(data = workshop_data, model = "angle", loglik_kind = "approx_differentiable", global_formula = "y ~ (1|participant_id)", include = [{"name": "a", "formula": "a ~ (1 + C(costly_fail_condition)|participant_id)"}], noncentered = False, )

Model initialized successfully.

In [49]:

AngleHierModelV2.graph()

AngleHierModelV2.graph()

Out[49]:

In [50]:

try:
    # Load pre-computed traces
    AngleHierModelV2.restore_traces(traces = "scientific_workflow_hssm/idata/angle_hier_v2/traces.nc")
except:
    # Sample posterior
    angle_hier_idata = AngleHierModelV2.sample(chains = 2,
                                             sampler = "nuts_numpyro",
                                             tune = 500,
                                             draws = 500,
                                            )

    # Sample posterior predictive
    AngleHierModelV2.sample_posterior_predictive(draws = 200,
                                                 safe_mode = True)

    # Save Model
    AngleHierModelV2.save_model(model_name = "angle_hier_v2",
                                allow_absolute_base_path = True,
                                base_path = "scientific_workflow_hssm/idata/",
                                save_idata_only = True)

try: # Load pre-computed traces AngleHierModelV2.restore_traces(traces = "scientific_workflow_hssm/idata/angle_hier_v2/traces.nc") except: # Sample posterior angle_hier_idata = AngleHierModelV2.sample(chains = 2, sampler = "nuts_numpyro", tune = 500, draws = 500, ) # Sample posterior predictive AngleHierModelV2.sample_posterior_predictive(draws = 200, safe_mode = True) # Save Model AngleHierModelV2.save_model(model_name = "angle_hier_v2", allow_absolute_base_path = True, base_path = "scientific_workflow_hssm/idata/", save_idata_only = True)

In [51]:

az.plot_trace(AngleHierModelV2.traces)
plt.tight_layout()

az.plot_trace(AngleHierModelV2.traces) plt.tight_layout()

In [52]:

az.plot_posterior(AngleHierModelV2.traces,
                  var_names = ["a_C(costly_fail_condition)|participant_id_mu"],
                  ref_val = 0,
                  kind = "hist",
                  ref_val_color = "red",
                  histtype = "step")

az.plot_posterior(AngleHierModelV2.traces, var_names = ["a_C(costly_fail_condition)|participant_id_mu"], ref_val = 0, kind = "hist", ref_val_color = "red", histtype = "step")

Out[52]:

<Axes: title={'center': 'a_C(costly_fail_condition)|participant_id_mu\n1'}>

In [53]:

# Posterior predictive
AngleHierModelV2.plot_posterior_predictive(step = True, 
                                           # row = 'participant_id',
                                           col = 'costly_fail_condition',
                                           bins = np.linspace(-5, 5, 50),
                                           )
plt.tight_layout()
plt.show()

# Posterior predictive AngleHierModelV2.plot_posterior_predictive(step = True, # row = 'participant_id', col = 'costly_fail_condition', bins = np.linspace(-5, 5, 50), ) plt.tight_layout() plt.show()

In [54]:

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV2, 
                                             cond="costly_fail_condition",
                                             )
ax.set_ylim(0, 3);

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV2, cond="costly_fail_condition", ) ax.set_ylim(0, 3);

Quite an improvement! Let's see what our quantitative model comparison metrics say.

Quantitative Model Comparison¶

In [55]:

az.compare(
    {"DDM": BasicDDMModel.traces,
     "DDM Hierarchical": DDMHierModel.traces,
     "Angle Hierarchical": AngleHierModel.traces,
     "Angle Hierarchical Cost": AngleHierModelV2.traces}
)

az.compare( {"DDM": BasicDDMModel.traces, "DDM Hierarchical": DDMHierModel.traces, "Angle Hierarchical": AngleHierModel.traces, "Angle Hierarchical Cost": AngleHierModelV2.traces} )

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/stats/stats.py:797: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.67 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

Out[55]:

	rank	elpd_loo	p_loo	elpd_diff	weight	se	dse	warning	scale
Angle Hierarchical Cost	0	-4470.826272	87.516854	0.000000	1.000000e+00	70.898643	0.000000	False	log
Angle Hierarchical	1	-4736.150740	78.295641	265.324468	2.313717e-07	72.823473	20.493430	False	log
DDM Hierarchical	2	-4954.407753	74.496783	483.581480	1.523141e-07	76.438410	25.173534	True	log
DDM	3	-5645.531361	4.771162	1174.705089	0.000000e+00	74.728599	40.610196	False	log

Good, we now incorporated the costly_fail_condition in a conceptually coherent manner.

Let's take a look at difficulty next.

In [56]:

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV2, 
                                             cond="quantile_difficulty_binary",
                                             )
ax.set_ylim(0, 3);

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV2, cond="quantile_difficulty_binary", ) ax.set_ylim(0, 3);

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/src/hssm/plotting/utils.py:327: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df.groupby(["observed", "chain", "draw", cond, "is_correct"])["rt"]
/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/src/hssm/plotting/utils.py:334: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df.groupby(["observed", "chain", "draw", cond])["is_correct"]

In [57]:

plot_rt_hists(workshop_data,
              by_participant = True,
              split_by_column = "quantile_difficulty_binary",
              inset_plot =  "rt_mean")

plot_rt_hists(workshop_data, by_participant = True, split_by_column = "quantile_difficulty_binary", inset_plot = "rt_mean")

/var/folders/gx/s43vynx550qbypcxm83fv56dzq4hgg/T/ipykernel_64548/900136031.py:142: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
  plt.tight_layout()

In [58]:

plot_rt_hists(workshop_data,
              by_participant = True,
              split_by_column = "quantile_difficulty_binary",
              inset_plot =  "choice_proportion")

plot_rt_hists(workshop_data, by_participant = True, split_by_column = "quantile_difficulty_binary", inset_plot = "choice_proportion")

/var/folders/gx/s43vynx550qbypcxm83fv56dzq4hgg/T/ipykernel_64548/900136031.py:142: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
  plt.tight_layout()

We see a similar pattern. Difficulty affects choice probability, however the effect on RT is less clear.

What parameter should difficulty map onto? Usually it maps onto the rate of evidence accumulation, which is the drift (v) parameter most SSMs.

We will move ahead and try this. To add specialized regression for v we can add another parameter dictionary to the list we pass to include.

Addressing difficulty¶

In [59]:

AngleHierModelV3 = hssm.HSSM(data = workshop_data,
                             model = "angle",
                             loglik_kind = "approx_differentiable",
                             global_formula = "y ~ (1|participant_id)",
                             include = [{"name": "a",
                                         "formula": "a ~ (1 + C(costly_fail_condition)|participant_id)"},
                                         {"name": "v",
                                         "formula": "v ~ (1 + continuous_difficulty|participant_id)"},
                                        ],
                             noncentered = False,
                            )

AngleHierModelV3 = hssm.HSSM(data = workshop_data, model = "angle", loglik_kind = "approx_differentiable", global_formula = "y ~ (1|participant_id)", include = [{"name": "a", "formula": "a ~ (1 + C(costly_fail_condition)|participant_id)"}, {"name": "v", "formula": "v ~ (1 + continuous_difficulty|participant_id)"}, ], noncentered = False, )

Model initialized successfully.

In [60]:

AngleHierModelV3.graph()

AngleHierModelV3.graph()

Out[60]:

In [61]:

try:
    # Load pre-computed traces
    AngleHierModelV3.restore_traces(traces = "scientific_workflow_hssm/idata/angle_hier_v3/traces.nc")
except:
    # Sample posterior
    angle_hier_idata = AngleHierModelV3.sample(chains = 2,
                                             sampler = "nuts_numpyro",
                                             tune = 500,
                                             draws = 500,
                                            )

    # Sample posterior predictive
    AngleHierModelV3.sample_posterior_predictive(draws = 200,
                                                 safe_mode = True)

    # Save Model
    AngleHierModelV3.save_model(model_name = "angle_hier_v3",
                                allow_absolute_base_path = True,
                                base_path = "scientific_workflow_hssm/idata/",
                                save_idata_only = True)

try: # Load pre-computed traces AngleHierModelV3.restore_traces(traces = "scientific_workflow_hssm/idata/angle_hier_v3/traces.nc") except: # Sample posterior angle_hier_idata = AngleHierModelV3.sample(chains = 2, sampler = "nuts_numpyro", tune = 500, draws = 500, ) # Sample posterior predictive AngleHierModelV3.sample_posterior_predictive(draws = 200, safe_mode = True) # Save Model AngleHierModelV3.save_model(model_name = "angle_hier_v3", allow_absolute_base_path = True, base_path = "scientific_workflow_hssm/idata/", save_idata_only = True)

In [62]:

az.plot_posterior(AngleHierModelV3.traces,
                  var_names = ["v_continuous_difficulty|participant_id_mu"],
                  ref_val = 0,
                  kind = "hist",
                  ref_val_color = "red",
                  histtype = "step")

az.plot_posterior(AngleHierModelV3.traces, var_names = ["v_continuous_difficulty|participant_id_mu"], ref_val = 0, kind = "hist", ref_val_color = "red", histtype = "step")

Out[62]:

<Axes: title={'center': 'v_continuous_difficulty|participant_id_mu'}>

Looks like the effect on v is small (to the trained eye :)), but it is significant! Let's check if we can account for the data pattern we missed previously.

In [63]:

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV3, 
                                             cond="quantile_difficulty_binary",
                                             )
ax.set_ylim(0, 3);

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV3, cond="quantile_difficulty_binary", ) ax.set_ylim(0, 3);

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/src/hssm/plotting/utils.py:327: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df.groupby(["observed", "chain", "draw", cond, "is_correct"])["rt"]
/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/src/hssm/plotting/utils.py:334: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df.groupby(["observed", "chain", "draw", cond])["is_correct"]

In [64]:

# Posterior predictive
AngleHierModelV3.plot_posterior_predictive(step = True, 
                                           col = "quantile_difficulty_binary",
                                           bins = np.linspace(-5,5, 50))
plt.tight_layout()

# Posterior predictive AngleHierModelV3.plot_posterior_predictive(step = True, col = "quantile_difficulty_binary", bins = np.linspace(-5,5, 50)) plt.tight_layout()

Success! This looks much better.

Quantitative Model Comparison¶

In [65]:

az.compare(
    {
     "DDM": BasicDDMModel.traces,
     "DDM Hierarchical": DDMHierModel.traces,
     "Angle Hierarchical": AngleHierModel.traces,
     "Angle Hierarchical Cost": AngleHierModelV2.traces,
     "Angle Hierarchical Cost/Diff": AngleHierModelV3.traces
     }
)

az.compare( { "DDM": BasicDDMModel.traces, "DDM Hierarchical": DDMHierModel.traces, "Angle Hierarchical": AngleHierModel.traces, "Angle Hierarchical Cost": AngleHierModelV2.traces, "Angle Hierarchical Cost/Diff": AngleHierModelV3.traces } )

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/stats/stats.py:797: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.67 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(
/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/stats/stats.py:797: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.67 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

Out[65]:

	rank	elpd_loo	p_loo	elpd_diff	weight	se	dse	warning	scale
Angle Hierarchical Cost/Diff	0	-4425.940827	69.185385	0.000000	9.876277e-01	70.554577	0.000000	True	log
Angle Hierarchical Cost	1	-4470.826272	87.516854	44.885445	1.237269e-02	70.898643	9.559271	False	log
Angle Hierarchical	2	-4736.150740	78.295641	310.209913	2.258851e-07	72.823473	22.959566	False	log
DDM Hierarchical	3	-4954.407753	74.496783	528.466926	1.496612e-07	76.438410	27.593021	True	log
DDM	4	-5645.531361	4.771162	1219.590534	0.000000e+00	74.728599	41.671983	False	log

Anything else?¶

At this point, we have a model that fits the data quite well.

We figured that a hierarchy significantly improves our fit, that the angle model dominates the basic ddm model for our data, and we incorporated effects based on our experiment manipulations.

A natural next step is to check for patterns based on more generic properties of human choice data that we may be able to reason about.

Anything that comes to mind? Let's take another look at our dataset for some inspiration.

In [66]:

workshop_data

workshop_data

Out[66]:

	response	rt	participant_id	trial	costly_fail_condition	continuous_difficulty	response_l1	bin_difficulty	quantile_difficulty	quantile_difficulty_binary	response_l1_plotting
0	1	0.556439	0	1	1	-0.277337	0	low	0	-1	1
1	1	0.741682	0	2	0	-0.810919	1	low	-1	-1	1
2	1	0.461832	0	3	0	-0.673330	1	low	-1	-1	1
3	1	0.626154	0	4	0	0.755445	1	high	1	1	1
4	1	0.651677	0	5	1	0.136755	1	high	0	1	1
...	...	...	...	...	...	...	...	...	...	...	...
4995	1	1.039342	19	246	0	-0.612223	-1	low	-1	-1	-1
4996	1	1.587827	19	247	0	0.732396	1	high	1	1	1
4997	1	0.668594	19	248	1	-0.175321	1	low	0	-1	1
4998	1	1.616471	19	249	0	-0.630447	1	low	-1	-1	1
4999	1	1.051329	19	250	1	0.511197	1	high	1	1	1

5000 rows × 11 columns

At risk of stating the obvious,we have a column that went unused thus far: response_l1, the lagged response.

Maybe this hints at some level of stickiness in the choice behavior? How could we incorporate this?

Let us first investigate if there is indeed such a pattern in the data!

In [67]:

# Posterior predictive
AngleHierModelV3.plot_posterior_predictive(step = True, 
                                           col = 'response_l1_plotting',
                                           bins = np.linspace(-5, 5, 50))
plt.tight_layout()

# Posterior predictive AngleHierModelV3.plot_posterior_predictive(step = True, col = 'response_l1_plotting', bins = np.linspace(-5, 5, 50)) plt.tight_layout()

Indeed, it does seem like there is a bit of a pattern here, that we miss so far!

To incoporate choice stickiness, a reasonable candidate parameter is z, the a priori choice bias. Maybe this parameter is affected by the last choice taken?

Let's try to incoporate this. We will

Addressing Stickyness¶

In [68]:

AngleHierModelV4 = hssm.HSSM(data = workshop_data,
                             model = "angle",
                             loglik_kind = "approx_differentiable",
                             global_formula = "y ~ (1|participant_id)",
                             include = [{"name": "a",
                                         "formula": "a ~ (1 + C(costly_fail_condition)|participant_id)"},
                                         {"name": "v",
                                          "formula": "v ~ (1 + continuous_difficulty|participant_id)"},
                                         {"name": "z",
                                          "formula": "z ~ (1 + response_l1|participant_id)"},
                                        ],
                             noncentered = False,
                            )

AngleHierModelV4 = hssm.HSSM(data = workshop_data, model = "angle", loglik_kind = "approx_differentiable", global_formula = "y ~ (1|participant_id)", include = [{"name": "a", "formula": "a ~ (1 + C(costly_fail_condition)|participant_id)"}, {"name": "v", "formula": "v ~ (1 + continuous_difficulty|participant_id)"}, {"name": "z", "formula": "z ~ (1 + response_l1|participant_id)"}, ], noncentered = False, )

Model initialized successfully.

In [69]:

AngleHierModelV4.graph()

AngleHierModelV4.graph()

Out[69]:

In [70]:

try:
    # Load pre-computed traces
    AngleHierModelV4.restore_traces(traces = "scientific_workflow_hssm/idata/angle_hier_v4/traces.nc")
except:
    # Sample posterior
    angle_hier_idata = AngleHierModelV4.sample(chains = 2,
                                             sampler = "nuts_numpyro",
                                             tune = 500,
                                             draws = 500,
                                            )

    # Sample posterior predictive
    AngleHierModelV4.sample_posterior_predictive(draws = 200,
                                                 safe_mode = True)

    # Save Model
    AngleHierModelV4.save_model(model_name = "angle_hier_v4",
                                allow_absolute_base_path = True,
                                base_path = "scientific_workflow_hssm/idata/",
                                save_idata_only = True)

try: # Load pre-computed traces AngleHierModelV4.restore_traces(traces = "scientific_workflow_hssm/idata/angle_hier_v4/traces.nc") except: # Sample posterior angle_hier_idata = AngleHierModelV4.sample(chains = 2, sampler = "nuts_numpyro", tune = 500, draws = 500, ) # Sample posterior predictive AngleHierModelV4.sample_posterior_predictive(draws = 200, safe_mode = True) # Save Model AngleHierModelV4.save_model(model_name = "angle_hier_v4", allow_absolute_base_path = True, base_path = "scientific_workflow_hssm/idata/", save_idata_only = True)

In [71]:

az.plot_trace(AngleHierModelV4.traces,
              divergences = None);
plt.tight_layout()

az.plot_trace(AngleHierModelV4.traces, divergences = None); plt.tight_layout()

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/plots/traceplot.py:223: UserWarning: rcParams['plot.max_subplots'] (20) is smaller than the number of variables to plot (24), generating only 20 plots
  warnings.warn(

** Note **:

We can see some rather interesting artifacts in the chains above. Around samples 300-375 it looks like our solid-blue chain got quite stuck. This indicates some problems with the posterior geometry for this model. One diagnostic that can be helpful here whether or not we observe a lot of divergences during sampling.

Let's take a look below (notice, we change the diveregences argument from None to it's default)

In [72]:

az.plot_trace(AngleHierModelV4.traces,
              divergences = 'auto');
plt.tight_layout()

az.plot_trace(AngleHierModelV4.traces, divergences = 'auto'); plt.tight_layout()

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/plots/traceplot.py:223: UserWarning: rcParams['plot.max_subplots'] (20) is smaller than the number of variables to plot (24), generating only 20 plots
  warnings.warn(

Indeed, we observe a fee divergences here... as rigorous scientists, we should now try to get to the bottom of this phenomenon (it happens often if one tries hierarchical models naively on real experimental data). In the context of this tutorial, we will let it slide however. It would warrant a longer detour.

Let's move on and focus on whether or not we actually identify a significant choice stickyness effect with our analysis:

In [73]:

az.plot_posterior(AngleHierModelV4.traces,
                  var_names = ["z_response_l1|participant_id_mu"],
                  ref_val = 0,
                  kind = "hist",
                  ref_val_color = "red",
                  histtype = "step")

az.plot_posterior(AngleHierModelV4.traces, var_names = ["z_response_l1|participant_id_mu"], ref_val = 0, kind = "hist", ref_val_color = "red", histtype = "step")

Out[73]:

<Axes: title={'center': 'z_response_l1|participant_id_mu'}>

We observe a significant effect on the z parameter, in fact a mean effect of 0.073 insinuate a fairly big effect of choice stickyness. In direct comparison, we might expect this effect to overall have a larger impact on our model fit than the effect of difficulty on v, which we investigated in the previous section.

In [74]:

# Posterior predictive
AngleHierModelV4.plot_posterior_predictive(step = True, 
                                           col = 'response_l1_plotting',
                                           bins = np.linspace(-5, 5, 50))
plt.tight_layout()

# Posterior predictive AngleHierModelV4.plot_posterior_predictive(step = True, col = 'response_l1_plotting', bins = np.linspace(-5, 5, 50)) plt.tight_layout()

Quantitative Model Comparison¶

In [75]:

az.compare(
    {"DDM": BasicDDMModel.traces,
     "DDM Hierarchical": DDMHierModel.traces,
     "Angle Hierarchical": AngleHierModel.traces,
     "Angle Hierarchical Cost": AngleHierModelV2.traces,
     "Angle Hierarchical Cost/Diff": AngleHierModelV3.traces,
     "Angle Hierarchical Cost/Diff/Sticky": AngleHierModelV4.traces}
)

az.compare( {"DDM": BasicDDMModel.traces, "DDM Hierarchical": DDMHierModel.traces, "Angle Hierarchical": AngleHierModel.traces, "Angle Hierarchical Cost": AngleHierModelV2.traces, "Angle Hierarchical Cost/Diff": AngleHierModelV3.traces, "Angle Hierarchical Cost/Diff/Sticky": AngleHierModelV4.traces} )

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/stats/stats.py:797: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.67 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(
/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/stats/stats.py:797: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.67 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

Out[75]:

	rank	elpd_loo	p_loo	elpd_diff	weight	se	dse	warning	scale
Angle Hierarchical Cost/Diff/Sticky	0	-4327.769237	103.455670	0.000000	0.918195	71.004980	0.000000	False	log
Angle Hierarchical Cost/Diff	1	-4425.940827	69.185385	98.171590	0.081805	70.554577	15.685768	True	log
Angle Hierarchical Cost	2	-4470.826272	87.516854	143.057036	0.000000	70.898643	17.113407	False	log
Angle Hierarchical	3	-4736.150740	78.295641	408.381504	0.000000	72.823473	26.073614	False	log
DDM Hierarchical	4	-4954.407753	74.496783	626.638516	0.000000	76.438410	29.304281	True	log
DDM	5	-5645.531361	4.771162	1317.762125	0.000000	74.728599	43.174373	False	log

And indeed, the drop inelpd_loo is even more substantial, than the improvement generated by incorporating the difficulty effect.

Taking Stock¶

In [76]:

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV4, 
                                             cond="response_l1_plotting",
                                             )
ax.set_ylim(0, 3);

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV4, cond="response_l1_plotting", ) ax.set_ylim(0, 3);

In [77]:

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV4, 
                                             cond="costly_fail_condition",
                                             )
ax.set_ylim(0, 3);

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV4, cond="costly_fail_condition", ) ax.set_ylim(0, 3);

In [78]:

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV4, 
                                             cond="quantile_difficulty_binary",
                                             )
ax.set_ylim(0, 3);

ax = hssm.plotting.plot_quantile_probability(AngleHierModelV4, cond="quantile_difficulty_binary", ) ax.set_ylim(0, 3);

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/src/hssm/plotting/utils.py:327: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df.groupby(["observed", "chain", "draw", cond, "is_correct"])["rt"]
/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/src/hssm/plotting/utils.py:334: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df.groupby(["observed", "chain", "draw", cond])["is_correct"]

Sanity Check, was the hierarchy really necessary¶

In [79]:

AngleModelV5 = hssm.HSSM(data = workshop_data,
                         model = "angle",
                         loglik_kind = "approx_differentiable",
                         global_formula = "y ~ 1",
                         include = [{"name": "a",
                                        "formula": "a ~ 1 + C(costly_fail_condition)"},
                                        {"name": "v",
                                        "formula": "v ~ 1 + continuous_difficulty"},
                                        {"name": "z",
                                        "formula": "z ~ 1 + response_l1"},
                                    ],
                         noncentered = False,
                         )

AngleModelV5 = hssm.HSSM(data = workshop_data, model = "angle", loglik_kind = "approx_differentiable", global_formula = "y ~ 1", include = [{"name": "a", "formula": "a ~ 1 + C(costly_fail_condition)"}, {"name": "v", "formula": "v ~ 1 + continuous_difficulty"}, {"name": "z", "formula": "z ~ 1 + response_l1"}, ], noncentered = False, )

Model initialized successfully.

In [80]:

try:
    # Load pre-computed traces
    AngleModelV5.restore_traces(traces = "scientific_workflow_hssm/idata/angle_v5/traces.nc")
except:
    # Sample posterior
    angle_hier_idata = AngleModelV5.sample(chains = 2,
                                           sampler = "nuts_numpyro",
                                           tune = 500,
                                           draws = 500,
                                           )

    # Sample posterior predictive
    AngleModelV5.sample_posterior_predictive(draws = 200,
                                                 safe_mode = True)

    # Save Model
    AngleModelV5.save_model(model_name = "angle_v5",
                            allow_absolute_base_path = True,
                            base_path = "scientific_workflow_hssm/idata/",
                            save_idata_only = True)

try: # Load pre-computed traces AngleModelV5.restore_traces(traces = "scientific_workflow_hssm/idata/angle_v5/traces.nc") except: # Sample posterior angle_hier_idata = AngleModelV5.sample(chains = 2, sampler = "nuts_numpyro", tune = 500, draws = 500, ) # Sample posterior predictive AngleModelV5.sample_posterior_predictive(draws = 200, safe_mode = True) # Save Model AngleModelV5.save_model(model_name = "angle_v5", allow_absolute_base_path = True, base_path = "scientific_workflow_hssm/idata/", save_idata_only = True)

In [81]:

az.compare(
    {
     "DDM": BasicDDMModel.traces,
     "DDM Hierarchical": DDMHierModel.traces,
     "Angle Hierarchical": AngleHierModel.traces,
     "Angle Hierarchical Cost": AngleHierModelV2.traces,
     "Angle Hierarchical Cost/Diff": AngleHierModelV3.traces,
     "Angle Hierarchical Cost/Diff/Sticky": AngleHierModelV4.traces,
     "Angle Cost/Diff/Sticky": AngleModelV5.traces
     }
)

az.compare( { "DDM": BasicDDMModel.traces, "DDM Hierarchical": DDMHierModel.traces, "Angle Hierarchical": AngleHierModel.traces, "Angle Hierarchical Cost": AngleHierModelV2.traces, "Angle Hierarchical Cost/Diff": AngleHierModelV3.traces, "Angle Hierarchical Cost/Diff/Sticky": AngleHierModelV4.traces, "Angle Cost/Diff/Sticky": AngleModelV5.traces } )

/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/stats/stats.py:797: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.67 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(
/Users/afengler/Library/CloudStorage/OneDrive-Personal/proj_hssm/HSSM/.venv/lib/python3.11/site-packages/arviz/stats/stats.py:797: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.67 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

Out[81]:

	rank	elpd_loo	p_loo	elpd_diff	weight	se	dse	warning	scale
Angle Hierarchical Cost/Diff/Sticky	0	-4327.769237	103.455670	0.000000	0.918195	71.004980	0.000000	False	log
Angle Hierarchical Cost/Diff	1	-4425.940827	69.185385	98.171590	0.081805	70.554577	15.685768	True	log
Angle Hierarchical Cost	2	-4470.826272	87.516854	143.057036	0.000000	70.898643	17.113407	False	log
Angle Hierarchical	3	-4736.150740	78.295641	408.381504	0.000000	72.823473	26.073614	False	log
DDM Hierarchical	4	-4954.407753	74.496783	626.638516	0.000000	76.438410	29.304281	True	log
Angle Cost/Diff/Sticky	5	-5001.726336	8.676713	673.957099	0.000000	70.471189	33.148987	False	log
DDM	6	-5645.531361	4.771162	1317.762125	0.000000	74.728599	43.174373	False	log

The End:¶

So far so good, we completed a rather comprehensive model exploration and we generated quite a few insights! We could obviously go on and try more and more complex models and maybe there is more to find out here... we leave this up to you and hope that HSSM will continue to help you along the way :).

Pointers to advanced Topics¶

We are scratching only the surface of what cann be done with HSSM, let alone the broader eco-system supporting simulation based inference (SBI).

Check out our simulator package, ssm-simulators as well as our our little neural network library for training LANs, lanfactory.

Exciting work is being done (more on this in the next tutorial) on connecting to other packages in the wider eco-system, such as BayesFlow as well as the sbi package.

Here is a taste of advanced topics with links to corresponding tutorials:

• Variational Inference with HSSM
• Build PyMC models with HSSM random variables
• Connect compiled models to third party MCMC libraries
• Construct custom models from simulators and contributed likelihoods
• Using link functions to transform parameters

you will find this and a lot more information in the official documentation