This tutorial provides a comprehensive introduction to the HSSM package for Hierarchical Bayesian Estimation of Sequential Sampling Models.

To make the most of the tutorial, let us cover the functionality of the key supporting packages that we use along the way.

Colab Instructions¶

If you would like to run this tutorial on Google colab, please click this link.

Once you are in the colab, follow the installation instructions below and then restart your runtime.

Just uncomment the code in the next code cell and run it!

NOTE:

You may want to switch your runtime to have a GPU or TPU. To do so, go to Runtime > Change runtime type and select the desired hardware accelerator.

Note that if you switch your runtime you have to follow the installation instructions again.

In [1]:

Copied!

# If running this on Colab, please uncomment the next line
# !pip install git+https://github.com/lnccbrown/HSSM@workshop_tutorial
# If running this on Colab, please uncomment the next line
# !pip install git+https://github.com/lnccbrown/HSSM@workshop_tutorial

Basic Imports¶

In [2]:

Copied!

import warnings

warnings.filterwarnings("ignore")
# warnings.filterwarnings(action='once')

# Basics

import numpy as np
from matplotlib import pyplot as plt

random_seed_sim = 134
np.random.seed(random_seed_sim)
import warnings

warnings.filterwarnings("ignore")
# warnings.filterwarnings(action='once')

# Basics

import numpy as np
from matplotlib import pyplot as plt

random_seed_sim = 134
np.random.seed(random_seed_sim)

Data Simulation¶

We will rely on the ssms package for data simulation repeatedly. Let's look at a basic isolated use case below.

As an example, let's use ssms to simulate from the basic Drift Diffusion Model (a running example in this tutorial).

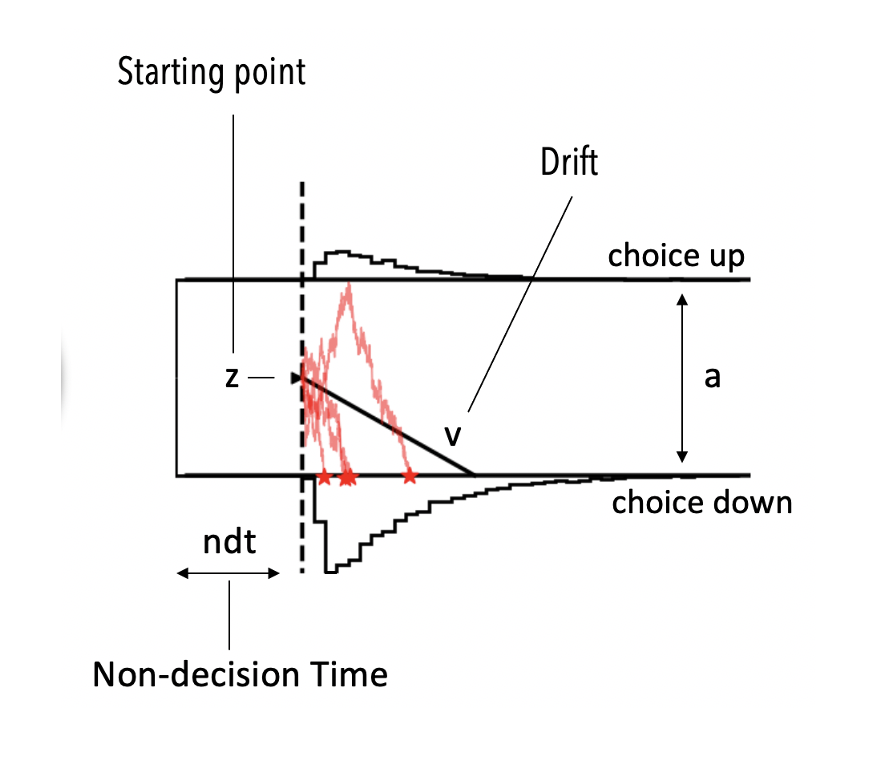
If you are not familiar with the DDM. For now just consider that it has four parameters.

v the drift rate
a the boundary separation
t the non-decision time
z the a priori decision bias (starting point)

Using `simulate_data()`¶

HSSM comes with a basic simulator function supplied the simulate_data() function. We can use this function to create synthetic datasets.

Below we show the most basic usecase:

We wish to generate 500 datapoints (trials) from the standard Drift Diffusion Model with a fixed parameters, v = 0.5, a = 1.5, z = 0.5, t = 0.5.

Note:

In the course of the tutorial, we will see multiple strategies for synthetic dataset generation, this being the most straightforward one.

In [3]:

Copied!





# Single dataset
import arviz as az  # Visualization
import bambi as bmb  # Model construction
import hddm_wfpt
import jax
import pytensor  # Graph-based tensor library

import hssm

pytensor.config.floatX = "float32"
jax.config.update("jax_enable_x64", False)

v_true = 0.5
a_true = 1.5
z_true = 0.5
t_true = 0.5

# Call the simulator function
dataset = hssm.simulate_data(
    model="ddm", theta=dict(v=v_true, a=a_true, z=z_true, t=t_true), size=500
)

dataset
# Single dataset
import arviz as az  # Visualization
import bambi as bmb  # Model construction
import hddm_wfpt
import jax
import pytensor  # Graph-based tensor library

import hssm

pytensor.config.floatX = "float32"
jax.config.update("jax_enable_x64", False)

v_true = 0.5
a_true = 1.5
z_true = 0.5
t_true = 0.5

# Call the simulator function
dataset = hssm.simulate_data(
    model="ddm", theta=dict(v=v_true, a=a_true, z=z_true, t=t_true), size=500
)

dataset

Out[3]:

	rt	response
0	1.508660	-1.0
1	2.240577	1.0
2	2.406826	1.0
3	1.313009	-1.0
4	2.382306	1.0
...	...	...
495	8.453332	1.0
496	1.206765	-1.0
497	0.980346	-1.0
498	5.192737	1.0
499	7.309368	1.0

500 rows × 2 columns

If instead you wish to supply a parameter that varies by trial (a lot more on this later), you can simply supply a vector of parameters to the theta dictionary, when calling the simulator.

Note:

The size argument conceptually functions as number of synthetic datasets. So if you supply a parameter as a (1000,) vector, then the simulator assumes that one dataset consists of 1000 trials, hence if we set the size = 1 as below, we expect in return a dataset with 1000 trials.

In [4]:

Copied!





# a changes trial wise
a_trialwise = np.random.normal(loc=2, scale=0.3, size=1000)

dataset_a_trialwise = hssm.simulate_data(
    model="ddm",
    theta=dict(
        v=v_true,
        a=a_trialwise,
        z=z_true,
        t=t_true,
    ),
    size=1,
)

dataset_a_trialwise
# a changes trial wise
a_trialwise = np.random.normal(loc=2, scale=0.3, size=1000)

dataset_a_trialwise = hssm.simulate_data(
    model="ddm",
    theta=dict(
        v=v_true,
        a=a_trialwise,
        z=z_true,
        t=t_true,
    ),
    size=1,
)

dataset_a_trialwise

Out[4]:

	rt	response
0	11.274393	1.0
1	1.466543	1.0
2	4.413692	1.0
3	2.083033	1.0
4	3.853630	1.0
...	...	...
995	7.015900	1.0
996	2.014142	1.0
997	6.252284	1.0
998	2.855168	1.0
999	6.931811	1.0

1000 rows × 2 columns

If we wish to simulate from another model, we can do so by changing the model string.

The number of models we can simulate differs from the number of models for which we have likelihoods available (both will increase over time). To get the models for which likelihood functions are supplied out of the box, we should check the SupportedModels under hssm.defaults.

In [5]:

Copied!

hssm.defaults.SupportedModels
hssm.defaults.SupportedModels

Out[5]:

typing.Literal['ddm', 'ddm_sdv', 'full_ddm', 'angle', 'levy', 'ornstein', 'weibull', 'race_no_bias_angle_4', 'ddm_seq2_no_bias']

If we wish to check more detailed information about a given model, we can use the default_model_config under hssm.default.

Let's look at the ddm:

In [6]:

Copied!

hssm.defaults.default_model_config["angle"]
hssm.defaults.default_model_config["angle"]

Out[6]:

{'response': ['rt', 'response'],
 'list_params': ['v', 'a', 'z', 't', 'theta'],
 'description': None,
 'likelihoods': {'approx_differentiable': {'loglik': 'angle.onnx',
   'backend': 'jax',
   'default_priors': {},
   'bounds': {'v': (-3.0, 3.0),
    'a': (0.3, 3.0),
    'z': (0.1, 0.9),
    't': (0.001, 2.0),
    'theta': (-0.1, 1.3)},
   'extra_fields': None}}}

This dictionary contains quite a bit of information. For purposes of simulating data from a given model, we will highlight two aspects:

The key list_of_params provides us with the necessary information to define out theta dictionary
The bounds key inside the likelihoods sub-dictionaries, provides us with an indication of reasonable parameter values.

The likelihoods dictionary inhabits three sub-directories for the ddm model, since we have all three, an analytical, an approx_differentiable (LAN) and a blackbox likelihood available. For many models, we will be able to access only one or two types of likelihoods.

Using `ssm-simulators`¶

Internally, HSSM natively makes use of the ssm-simulators package for forward simulation of models. hssm.simulate_data() functions essentially as a convenience-wrapper.

Below we illustrate how to simulate data using the ssm-simulators package directly, to generate an equivalent dataset as created above. We will use the third way of passing parameters to the simulator, which is as a parameter-matrix.

Notes:

If you pass parameters as a parameter matrix, make sure the column ordering is correct. You can follow the parameter ordering under hssm.defaults.default_model_config['ddm']['list_params'].
This is a minimal example, for more information about the package, check the associated github-page.

In [7]:

Copied!





import numpy as np
import pandas as pd
from ssms.basic_simulators.simulator import simulator

# a changes trial wise
theta_mat = np.zeros((1000, 4))
theta_mat[:, 0] = v_true  # v
theta_mat[:, 1] = a_trialwise  # a
theta_mat[:, 2] = z_true  # z
theta_mat[:, 3] = t_true  # t

# simulate data
sim_out_trialwise = simulator(
    theta=theta_mat,  # parameter_matrix
    model="ddm",  # specify model (many are included in ssms)
    n_samples=1,  # number of samples for each set of parameters
    # (plays the role of `size` parameter in `hssm.simulate_data`)
)

# Turn into nice dataset
dataset_trialwise = pd.DataFrame(
    np.column_stack(
        [sim_out_trialwise["rts"][:, 0], sim_out_trialwise["choices"][:, 0]]
    ),
    columns=["rt", "response"],
)

dataset_trialwise
import numpy as np
import pandas as pd
from ssms.basic_simulators.simulator import simulator

# a changes trial wise
theta_mat = np.zeros((1000, 4))
theta_mat[:, 0] = v_true  # v
theta_mat[:, 1] = a_trialwise  # a
theta_mat[:, 2] = z_true  # z
theta_mat[:, 3] = t_true  # t

# simulate data
sim_out_trialwise = simulator(
    theta=theta_mat,  # parameter_matrix
    model="ddm",  # specify model (many are included in ssms)
    n_samples=1,  # number of samples for each set of parameters
    # (plays the role of `size` parameter in `hssm.simulate_data`)
)

# Turn into nice dataset
dataset_trialwise = pd.DataFrame(
    np.column_stack(
        [sim_out_trialwise["rts"][:, 0], sim_out_trialwise["choices"][:, 0]]
    ),
    columns=["rt", "response"],
)

dataset_trialwise

Out[7]:

	rt	response
0	11.274393	1.0
1	1.466543	1.0
2	4.413692	1.0
3	2.083033	1.0
4	3.853630	1.0
...	...	...
995	7.015900	1.0
996	2.014142	1.0
997	6.252284	1.0
998	2.855168	1.0
999	6.931811	1.0

1000 rows × 2 columns

We will stick to hssm.simulate_data() in this tutorial, to keep things simple.

ArviZ for Plotting¶

We use the ArviZ package for most of our plotting needs. ArviZ is a useful aid for plotting when doing anything Bayesian.

It works with HSSM out of the box, by virtue of HSSMs reliance on PyMC for model construction and sampling.

Checking out the ArviZ Documentation is a good idea to give you communication superpowers for not only your HSSM results, but also other libraries in the Bayesian Toolkit such as NumPyro or STAN.

We will see ArviZ plots throughout the notebook.

Main Tutorial¶

Initial Dataset¶

Let's proceed to simulate a simple dataset for our first example.

In [8]:

Copied!





# Specify
param_dict_init = dict(
    v=v_true,
    a=a_true,
    z=z_true,
    t=t_true,
)


dataset = hssm.simulate_data(
    model="ddm",
    theta=param_dict_init,
    size=500,
)

dataset
# Specify
param_dict_init = dict(
    v=v_true,
    a=a_true,
    z=z_true,
    t=t_true,
)


dataset = hssm.simulate_data(
    model="ddm",
    theta=param_dict_init,
    size=500,
)

dataset

Out[8]:

	rt	response
0	1.508660	-1.0
1	2.240577	1.0
2	2.406826	1.0
3	1.313009	-1.0
4	2.382306	1.0
...	...	...
495	8.453332	1.0
496	1.206765	-1.0
497	0.980346	-1.0
498	5.192737	1.0
499	7.309368	1.0

500 rows × 2 columns

First HSSM Model¶

In this example we will use the analytical likelihood function computed as suggested in this paper.

Instantiate the model¶

To instantiate our HSSM class, in the simplest version, we only need to provide an appropriate dataset. The dataset is expected to be a pandas.DataFrame with at least two columns, respectively called rt (for reaction time) and response. Our data simulated above is already in the correct format, so let us try to construct the class.

NOTE:

If you are a user of the HDDM python package, this workflow should seem very familiar.

In [9]:

Copied!

simple_ddm_model = hssm.HSSM(data=dataset)
simple_ddm_model = hssm.HSSM(data=dataset)

{'t_log__': array(0.6931472, dtype=float32), 'a_log__': array(0.6931472, dtype=float32), 'z_interval__': array(0., dtype=float32), 'v': array(0., dtype=float32)}

In [10]:

Copied!

simple_ddm_model
simple_ddm_model

Out[10]:

Hierarchical Sequential Sampling Model
Model: ddm

Response variable: rt,response
Likelihood: analytical
Observations: 500

Parameters:

v:
    Formula: None
    Priors:
        v ~ Normal(mu: 0.0, sigma: 2.5)
    Link: None
    Explicit bounds: (-inf, inf)

a:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)

z:
    Prior: Uniform(lower: 0.0, upper: 1.0)
    Explicit bounds: (0.0, 1.0)

t:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)


Lapse probability: 0.05
Lapse distribution: Uniform(lower: 0.0, upper: 20.0)

The print() function gives us some basic information about our model including the number of observations the parameters in the model and their respective prior setting. We can also create a nice little graphical representation of our model...

Model Graph¶

Since HSSM creates a PyMC Model, we can can use the .graph() function, to get a graphical representation of the the model we created.

In [11]:

Copied!

simple_ddm_model.graph()
simple_ddm_model.graph()

Out[11]:

This is the simplest model we can build. The graph above follows plate notation, commonly used for probabilistic graphical models.

We have our basic parameters (unobserved, white nodes), these are random variables in the model and we want to estimate them
Our observed reaction times and choices (SSMRandomVariable, grey node), are fixed (or conditioned on).
Rounded rectangles provide us with information about dimensionality of objects
Rectangles with sharp edges represent deterministic, but computed quantities (not shown here, but in later models)

This notation is helpful to get a quick overview of the structure of a given model we construct.

The graph() function of course becomes a lot more interesting and useful for more complicated models!

Sample from the Model¶

We can now call the .sample() function, to get posterior samples. The main arguments you may want to change are listed in the function call below.

Importantly, multiple backends are possible. We choose the nuts_numpyro backend below, which in turn compiles the model to a JAX function.

In [12]:

Copied!





infer_data_simple_ddm_model = simple_ddm_model.sample(
    sampler="nuts_numpyro",  # type of sampler to choose, 'nuts_numpyro',
    # 'nuts_blackjax' of default pymc nuts sampler
    cores=1,  # how many cores to use
    chains=2,  # how many chains to run
    draws=500,  # number of draws from the markov chain
    tune=1000,  # number of burn-in samples
    idata_kwargs=dict(log_likelihood=True),  # return log likelihood
)  # mp_ctx="forkserver")
infer_data_simple_ddm_model = simple_ddm_model.sample(
    sampler="nuts_numpyro",  # type of sampler to choose, 'nuts_numpyro',
    # 'nuts_blackjax' of default pymc nuts sampler
    cores=1,  # how many cores to use
    chains=2,  # how many chains to run
    draws=500,  # number of draws from the markov chain
    tune=1000,  # number of burn-in samples
    idata_kwargs=dict(log_likelihood=True),  # return log likelihood
)  # mp_ctx="forkserver")

Using default initvals.

  0%|          | 0/1500 [00:00<?, ?it/s]

  0%|          | 0/1500 [00:00<?, ?it/s]

We recommend running at least 4 chains for robust computation of convergence diagnostics

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x2a7202d50>
PERFORMING PREDICTION

Output()

We sampled from the model, let's look at the output...

In [13]:

Copied!

type(infer_data_simple_ddm_model)
type(infer_data_simple_ddm_model)

Out[13]:

arviz.data.inference_data.InferenceData

Errr... a closer look might be needed here!

Inference Data / What gets returned from the sampler?¶

The sampler returns an ArviZ InferenceData object.

To understand all the logic behind these objects and how they mesh with the Bayesian Workflow, we refer you to the ArviZ Documentation.

InferenceData is build on top of xarrays. The xarray documentation will help you understand in more detail how to manipulate these objects.

But let's take a quick high-level look to understand roughly what we are dealing with here!

We see that in our case, infer_data_simple_ddm_model contains four basic types of data (note: this is extensible!)

posterior
log_likelihood
sample_stats
observed_data

The posterior object contains our traces for each of the parameters in the model. The log_likelihood field contains the trial wise log-likelihoods for each sample from the posterior. The sample_stats field contains information about the sampler run. This can be important for chain diagnostics, but we will not dwell on this here. Finally we retreive our observed_data.

Basic Manipulation¶

Accessing groups and variables¶

To simply access the underlying data as a numpy.ndarray, we can use .values (as e.g. when using pandas.DataFrame objects).

In [17]:

Copied!

type(infer_data_simple_ddm_model.posterior.a.values)
type(infer_data_simple_ddm_model.posterior.a.values)

Out[17]:

numpy.ndarray

In [18]:

Copied!

# infer_data_simple_ddm_model.posterior.a.values
# infer_data_simple_ddm_model.posterior.a.values

Combine `chain` and `draw` dimension¶

When operating directly on the xarray, you will often find it useful to collapse the chain and draw coordinates into a single coordinate. Arviz makes this easy via the extract method.

Since Arviz really just calls the .stack() method from xarray, here the corresponding example using the lower level xarray interface.

Making use of ArviZ¶

Working with the InferenceData directly, is very helpful if you want to include custom computations into your workflow. For a basic Bayesian Workflow however, you will often find that standard functionality available through ArviZ suffices.

Below we provide a few examples of useful Arviz outputs, which come handy for analyzing your traces (MCMC samples).

Summary table¶

Let's take a look at a summary table for our posterior.

In [21]:

Copied!





az.summary(
    infer_data_simple_ddm_model,
    var_names=[var_name.name for var_name in simple_ddm_model.pymc_model.free_RVs],
)
az.summary(
    infer_data_simple_ddm_model,
    var_names=[var_name.name for var_name in simple_ddm_model.pymc_model.free_RVs],
)

Out[21]:

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
t	0.529	0.029	0.473	0.579	0.001	0.001	623.0	630.0	1.00
a	1.497	0.038	1.431	1.569	0.001	0.001	739.0	703.0	1.01
z	0.516	0.018	0.486	0.552	0.001	0.001	536.0	770.0	1.00
v	0.478	0.043	0.402	0.560	0.002	0.001	635.0	719.0	1.00

This table returns the parameter-wise mean of our posterior and a few extra statistics.

Of these extra statistics, the one-stop shop for flagging convergence issues is the r_hat value, which is reported in the right-most column.

To navigate this statistic, here is a rule of thumb widely used in applied Bayesian statistics.

If you find an r_hat value > 1.01, it warrants investigation.

Trace plot¶

In [22]:

Copied!





az.plot_trace(
    infer_data_simple_ddm_model,  # we exclude the log_likelihood traces here
    lines=[(key_, {}, param_dict_init[key_]) for key_ in param_dict_init],
)
plt.tight_layout()
az.plot_trace(
    infer_data_simple_ddm_model,  # we exclude the log_likelihood traces here
    lines=[(key_, {}, param_dict_init[key_]) for key_ in param_dict_init],
)
plt.tight_layout()

The .sample() function also sets a trace attribute, on our hssm class, so instead, we could call the plot like so:

In [23]:

Copied!





az.plot_trace(
    simple_ddm_model.traces,
    lines=[(key_, {}, param_dict_init[key_]) for key_ in param_dict_init],
);
az.plot_trace(
    simple_ddm_model.traces,
    lines=[(key_, {}, param_dict_init[key_]) for key_ in param_dict_init],
);

In this tutorial we are most often going to use the latter way of accessing the traces, but there is no preferred option.

Let's look at a few more plots.

Forest Plot¶

The forest plot is commonly used for a quick visual check of the marginal posteriors. It is very effective for intuitive communication of results.

In [24]:

Copied!

az.plot_forest(simple_ddm_model.traces)
az.plot_forest(simple_ddm_model.traces)

Out[24]:

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

Combining Chains¶

By default, chains are separated out into separate caterpillars, however sometimes, especially if you are looking at a forest plot which includes many posterior parameters at once, you want to declutter and collapse the chains into single caterpillars. In this case you can combine chains instead.

In [25]:

Copied!

az.plot_forest(simple_ddm_model.traces, combined=True)
az.plot_forest(simple_ddm_model.traces, combined=True)

Out[25]:

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

Basic Marginal Posterior Plot¶

Another way to view the marginal posteriors is provided by the plot_posterior() function. It shows the mean and by default the $94\%$ HDIs.

In [26]:

Copied!

az.plot_posterior(simple_ddm_model.traces)
az.plot_posterior(simple_ddm_model.traces)

Out[26]:

array([<Axes: title={'center': 'a'}>, <Axes: title={'center': 't'}>,
       <Axes: title={'center': 'v'}>, <Axes: title={'center': 'z'}>],
      dtype=object)

Especially for parameter recovery studies, you may want to include reference values for the parameters of interest.

You can do so using the ref_val argument. See the example below:

In [27]:

Copied!





az.plot_posterior(
    simple_ddm_model.traces,
    ref_val=[
        param_dict_init[var_name]
        for var_name in simple_ddm_model.traces.posterior.data_vars
    ],
)
az.plot_posterior(
    simple_ddm_model.traces,
    ref_val=[
        param_dict_init[var_name]
        for var_name in simple_ddm_model.traces.posterior.data_vars
    ],
)

Out[27]:

array([<Axes: title={'center': 'a'}>, <Axes: title={'center': 't'}>,
       <Axes: title={'center': 'v'}>, <Axes: title={'center': 'z'}>],
      dtype=object)

Since it is sometimes useful, especially for more complex cases, below an alternative approach in which we pass ref_val as a dictionary.

In [28]:

Copied!





az.plot_posterior(
    simple_ddm_model.traces,
    ref_val={
        "v": [{"ref_val": param_dict_init["v"]}],
        "a": [{"ref_val": param_dict_init["a"]}],
        "z": [{"ref_val": param_dict_init["z"]}],
        "t": [{"ref_val": param_dict_init["t"]}],
    },
)
az.plot_posterior(
    simple_ddm_model.traces,
    ref_val={
        "v": [{"ref_val": param_dict_init["v"]}],
        "a": [{"ref_val": param_dict_init["a"]}],
        "z": [{"ref_val": param_dict_init["z"]}],
        "t": [{"ref_val": param_dict_init["t"]}],
    },
)

Out[28]:

array([<Axes: title={'center': 'a'}>, <Axes: title={'center': 't'}>,
       <Axes: title={'center': 'v'}>, <Axes: title={'center': 'z'}>],
      dtype=object)

Posterior Pair Plot¶

The posterior pair plot show us bi-variate traceplots and is useful to check for simple parameter tradeoffs that may emerge. The simplest (linear) tradeoff may be a high correlation between two parameters. This can be very helpful in diagnosing sampler issues for example. If such tradeoffs exist, one often see extremely wide marginal distributions.

In our ddm example, we see a little bit of a tradeoff between a and t, as well as between v and z, however nothing concerning.

In [29]:

Copied!





az.plot_pair(
    simple_ddm_model.traces,
    kind="kde",
    reference_values=param_dict_init,
    marginals=True,
);
az.plot_pair(
    simple_ddm_model.traces,
    kind="kde",
    reference_values=param_dict_init,
    marginals=True,
);

The few plot we showed here are just the beginning: ArviZ has a much broader spectrum of graphs and other convenience function available. Just check the documentation.

Compute Quantities from idata¶

Example: Mean and Covariance of Posterior Parameters¶

As a simple example, let us calculate the covariance matrix for our posterior samples.

In [30]:

Copied!





# Calculate the correlation matrix
posterior_correlation_matrix = np.corrcoef(
    np.stack(
        [idata_extracted[var_].values for var_ in idata_extracted.data_vars.variables]
    )
)
num_vars = posterior_correlation_matrix.shape[0]

# Make heatmap
fig, ax = plt.subplots(1, 1)
cax = ax.imshow(posterior_correlation_matrix, cmap="coolwarm", vmin=-1, vmax=1)
fig.colorbar(cax, ax=ax)
ax.set_title("Posterior Correlation Matrix")

# Add ticks
ax.set_xticks(range(posterior_correlation_matrix.shape[0]))
ax.set_xticklabels([var_ for var_ in idata_extracted.data_vars.variables])
ax.set_yticks(range(posterior_correlation_matrix.shape[0]))
ax.set_yticklabels([var_ for var_ in idata_extracted.data_vars.variables])

# Annotate heatmap
for i in range(num_vars):
    for j in range(num_vars):
        ax.text(
            j,
            i,
            f"{posterior_correlation_matrix[i, j]:.2f}",
            ha="center",
            va="center",
            color="black",
        )

plt.show()
# Calculate the correlation matrix
posterior_correlation_matrix = np.corrcoef(
    np.stack(
        [idata_extracted[var_].values for var_ in idata_extracted.data_vars.variables]
    )
)
num_vars = posterior_correlation_matrix.shape[0]

# Make heatmap
fig, ax = plt.subplots(1, 1)
cax = ax.imshow(posterior_correlation_matrix, cmap="coolwarm", vmin=-1, vmax=1)
fig.colorbar(cax, ax=ax)
ax.set_title("Posterior Correlation Matrix")

# Add ticks
ax.set_xticks(range(posterior_correlation_matrix.shape[0]))
ax.set_xticklabels([var_ for var_ in idata_extracted.data_vars.variables])
ax.set_yticks(range(posterior_correlation_matrix.shape[0]))
ax.set_yticklabels([var_ for var_ in idata_extracted.data_vars.variables])

# Annotate heatmap
for i in range(num_vars):
    for j in range(num_vars):
        ax.text(
            j,
            i,
            f"{posterior_correlation_matrix[i, j]:.2f}",
            ha="center",
            va="center",
            color="black",
        )

plt.show()

HSSM Model based on LAN likelihood¶

With HSSM you can switch between pre-supplied models with a simple change of argument. The type of likelihood that will be accessed might change in the background for you.

Here we see an example in which the underlying likelihood is now a LAN.

We will talk more about different types of likelihood functions and backends later in the tutorial. For now just keep the following in mind:

There are three types of likelihoods

analytic
approx_differentiable
blackbox

To check which type is used in your HSSM model simple type:

In [31]:

Copied!

simple_ddm_model.loglik_kind
simple_ddm_model.loglik_kind

Out[31]:

'analytical'

Ah... we were using an analytical likelihood with the DDM model in the last section. Now let's see something different!

Simulating Angle Data¶

Again, let us simulate a simple dataset. This time we will use the angle model (passed via the model argument to the simulator() function).

This model is distinguished from the basic ddm model by an additional theta parameter which specifies the angle with which the decision boundaries collapse over time.

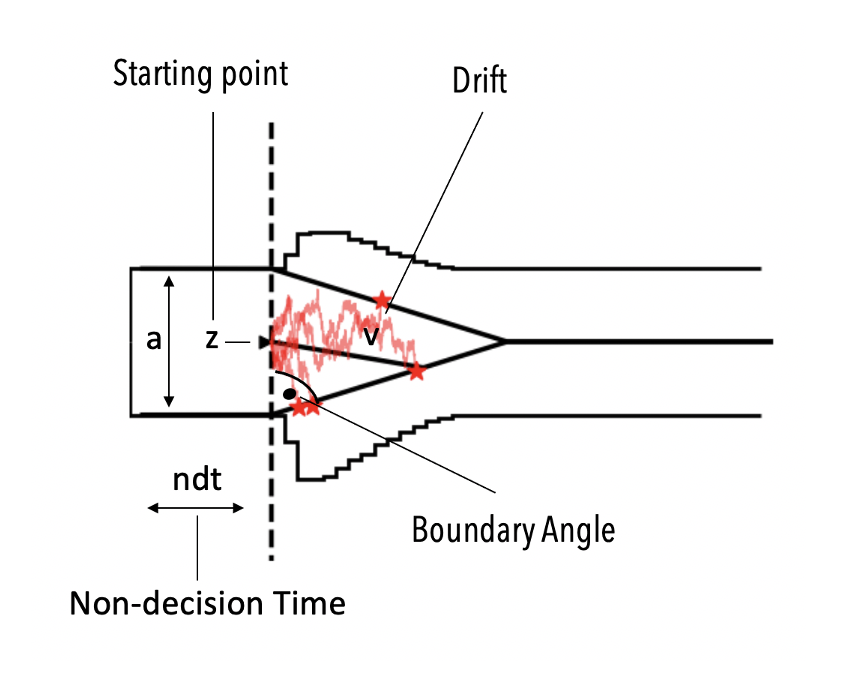
DDMs with collapsing bounds have been of significant interest in the theoretical literature, but applications were rare due to a lack of analytical likelihoods. HSSM facilitates inference with such models via the our approx_differentiable likelihoods. HSSM ships with a few predefined models based on LANs, but really we don't want to overemphasize those. They reflect the research interest of our and adjacent labs to a great extend.

Instead, we encourage the community to contribute to this model reservoir (more on this later).

In [32]:

Copied!





# Simulate angle data
v_angle_true = 0.5
a_angle_true = 1.5
z_angle_true = 0.5
t_angle_true = 0.2
theta_angle_true = 0.2

param_dict_angle = dict(v=0.5, a=1.5, z=0.5, t=0.2, theta=0.2)

lines_list_angle = [(key_, {}, param_dict_angle[key_]) for key_ in param_dict_angle]

dataset_angle = hssm.simulate_data(model="angle", theta=param_dict_angle, size=1000)
# Simulate angle data
v_angle_true = 0.5
a_angle_true = 1.5
z_angle_true = 0.5
t_angle_true = 0.2
theta_angle_true = 0.2

param_dict_angle = dict(v=0.5, a=1.5, z=0.5, t=0.2, theta=0.2)

lines_list_angle = [(key_, {}, param_dict_angle[key_]) for key_ in param_dict_angle]

dataset_angle = hssm.simulate_data(model="angle", theta=param_dict_angle, size=1000)

We pass a single additional argument to our HSSM class and set model='angle'.

In [33]:

Copied!

model_angle = hssm.HSSM(data=dataset_angle, model="angle")

model_angle
model_angle = hssm.HSSM(data=dataset_angle, model="angle")

model_angle

{'a_interval__': array(-8.940697e-08, dtype=float32), 't_interval__': array(-5.9604645e-08, dtype=float32), 'z_interval__': array(1.1920929e-07, dtype=float32), 'theta_interval__': array(0., dtype=float32), 'v': array(0., dtype=float32)}

Out[33]:

Hierarchical Sequential Sampling Model
Model: angle

Response variable: rt,response
Likelihood: approx_differentiable
Observations: 1000

Parameters:

v:
    Formula: None
    Priors:
        v ~ Normal(mu: 0.0, sigma: 2.5)
    Link: None
    Explicit bounds: (-3.0, 3.0)

a:
    Prior: Uniform(lower: 0.30000001192092896, upper: 3.0)
    Explicit bounds: (0.3, 3.0)

z:
    Prior: Uniform(lower: 0.10000000149011612, upper: 0.8999999761581421)
    Explicit bounds: (0.1, 0.9)

t:
    Prior: Uniform(lower: 0.0010000000474974513, upper: 2.0)
    Explicit bounds: (0.001, 2.0)

theta:
    Prior: Uniform(lower: -0.10000000149011612, upper: 1.2999999523162842)
    Explicit bounds: (-0.1, 1.3)


Lapse probability: 0.05
Lapse distribution: Uniform(lower: 0.0, upper: 20.0)

The model graph now show us an additional parameter theta!

In [34]:

Copied!

model_angle.graph()
model_angle.graph()

Out[34]:

Let's check the type of likelihood that is used under the hood ...

In [35]:

Copied!

model_angle.loglik_kind
model_angle.loglik_kind

Out[35]:

'approx_differentiable'

Ok so here we rely on a likelihood of the approx_differentiable kind.

As discussed, with the initial set of pre-supplied likelihoods, this implies that we are using a LAN in the background.

In [36]:

Copied!





jax.config.update("jax_enable_x64", False)
infer_data_angle = model_angle.sample(
    sampler="nuts_numpyro",
    chains=2,
    cores=2,
    draws=500,
    tune=500,
    idata_kwargs=dict(log_likelihood=False),  # no need to return likelihoods here
)
jax.config.update("jax_enable_x64", False)
infer_data_angle = model_angle.sample(
    sampler="nuts_numpyro",
    chains=2,
    cores=2,
    draws=500,
    tune=500,
    idata_kwargs=dict(log_likelihood=False),  # no need to return likelihoods here
)

Using default initvals.

  0%|          | 0/1000 [00:00<?, ?it/s]

  0%|          | 0/1000 [00:00<?, ?it/s]

We recommend running at least 4 chains for robust computation of convergence diagnostics
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x2f842dc50>
PERFORMING PREDICTION

In [37]:

Copied!

az.plot_trace(model_angle.traces, lines=lines_list_angle)
plt.tight_layout()
az.plot_trace(model_angle.traces, lines=lines_list_angle)
plt.tight_layout()

Choosing Priors¶

HSSM allows you to specify priors quite freely. If you used HDDM previously, you may feel relieved to read that your hands are now untied!

With HSSM we have multiple routes to priors. But let's first consider a special case:

Fixing a parameter to a given value¶

Assume that instead of fitting all parameters of the DDM,

we instead want to fit only the v (drift) parameter, setting all other parameters to fixed scalar values.

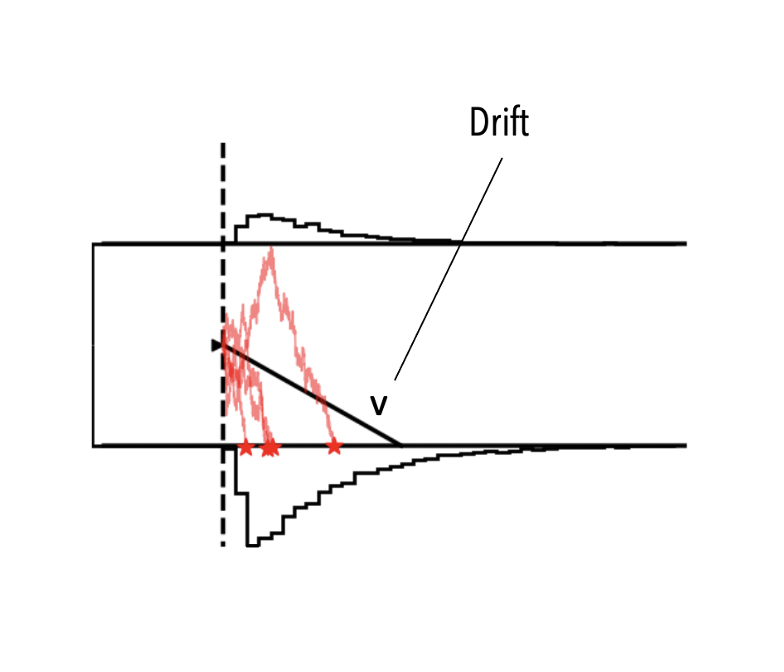
HSSM makes this extremely easy!

In [38]:

Copied!

param_dict_init
param_dict_init

Out[38]:

{'v': 0.5, 'a': 1.5, 'z': 0.5, 't': 0.5}

In [39]:

Copied!





ddm_model_only_v = hssm.HSSM(
    data=dataset,
    model="ddm",
    a=param_dict_init["a"],
    t=param_dict_init["t"],
    z=param_dict_init["z"],
)
ddm_model_only_v = hssm.HSSM(
    data=dataset,
    model="ddm",
    a=param_dict_init["a"],
    t=param_dict_init["t"],
    z=param_dict_init["z"],
)

{'v': array(0., dtype=float32)}

Since we fix all but one parameter, we therefore estimate only one parameter. This should be reflected in our model graph, where we expect only one free random variable v:

In [40]:

Copied!

ddm_model_only_v.graph()
ddm_model_only_v.graph()

Out[40]:

In [42]:

Copied!

az.plot_trace(
    ddm_model_only_v.traces.posterior, lines=[("v", {}, param_dict_init["v"])]
);
az.plot_trace(
    ddm_model_only_v.traces.posterior, lines=[("v", {}, param_dict_init["v"])]
);

Instead of the trace on the right, a useful alternative / complement is the rank plot. As a rule of thumb, if the rank plots within chains look uniformly distributed, then our chains generally exhibit good mixing.

In [43]:

Copied!

az.plot_trace(ddm_model_only_v.traces, kind="rank_bars")
az.plot_trace(ddm_model_only_v.traces, kind="rank_bars")

Out[43]:

array([[<Axes: title={'center': 'v'}>,
        <Axes: title={'center': 'v'}, xlabel='Rank (all chains)', ylabel='Chain'>]],
      dtype=object)

Named priors¶

We can choose any PyMC Distribution to specify a prior for a given parameter.

Even better, if natural parameter bounds are provided, HSSM automatically truncates the prior distribution so that it respect these bounds.

Below is an example in which we specify a Normal prior on the v parameter of the DDM.

We choose a ridiculously low $\sigma$ value, to illustrate it's regularizing effect on the parameter (just so we see a difference and you are convinced that something changed).

In [44]:

Copied!





model_normal = hssm.HSSM(
    data=dataset,
    include=[
        {
            "name": "v",
            "prior": {"name": "Normal", "mu": 0, "sigma": 0.01},
        }
    ],
)
model_normal = hssm.HSSM(
    data=dataset,
    include=[
        {
            "name": "v",
            "prior": {"name": "Normal", "mu": 0, "sigma": 0.01},
        }
    ],
)

{'t_log__': array(0.6931472, dtype=float32), 'a_log__': array(0.6931472, dtype=float32), 'z_interval__': array(0., dtype=float32), 'v': array(0., dtype=float32)}

In [45]:

Copied!

model_normal
model_normal

Out[45]:

Hierarchical Sequential Sampling Model
Model: ddm

Response variable: rt,response
Likelihood: analytical
Observations: 500

Parameters:

v:
    Formula: None
    Priors:
        v ~ Normal(mu: 0.0, sigma: 2.5)
    Link: None
    Explicit bounds: (-inf, inf)

a:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)

z:
    Prior: Uniform(lower: 0.0, upper: 1.0)
    Explicit bounds: (0.0, 1.0)

t:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)


Lapse probability: 0.05
Lapse distribution: Uniform(lower: 0.0, upper: 20.0)

In [46]:

Copied!





infer_data_normal = model_normal.sample(
    sampler="nuts_numpyro",
    chains=2,
    cores=2,
    draws=500,
    tune=500,
    idata_kwargs=dict(log_likelihood=False),  # no need to return likelihoods here
)
infer_data_normal = model_normal.sample(
    sampler="nuts_numpyro",
    chains=2,
    cores=2,
    draws=500,
    tune=500,
    idata_kwargs=dict(log_likelihood=False),  # no need to return likelihoods here
)

Using default initvals.

  0%|          | 0/1000 [00:00<?, ?it/s]

  0%|          | 0/1000 [00:00<?, ?it/s]

We recommend running at least 4 chains for robust computation of convergence diagnostics

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x2b9370a90>
PERFORMING PREDICTION

In [47]:

Copied!





az.plot_trace(
    model_normal.traces,
    lines=[(key_, {}, param_dict_init[key_]) for key_ in param_dict_init],
)
az.plot_trace(
    model_normal.traces,
    lines=[(key_, {}, param_dict_init[key_]) for key_ in param_dict_init],
)

Out[47]:

array([[<Axes: title={'center': 'a'}>, <Axes: title={'center': 'a'}>],
       [<Axes: title={'center': 't'}>, <Axes: title={'center': 't'}>],
       [<Axes: title={'center': 'v'}>, <Axes: title={'center': 'v'}>],
       [<Axes: title={'center': 'z'}>, <Axes: title={'center': 'z'}>]],
      dtype=object)

Observe how we reused our previous dataset with underlying parameters

v = 0.5
a = 1.5
z = 0.5
t = 0.2

In contrast to our previous sampler round, in which we used Uniform priors, here the v estimate is shrunk severley towared $0$ and the t and z parameter estimates are very biased to make up for this distortion.

HSSM Model with Regression¶

Crucial to the scope of HSSM is the ability to link parameters with trial-by-trial covariates via (hierarchical, but more on this later) general linear models.

In this section we explore how HSSM deals with these models. No big surprise here... it's simple!

Case 1: One parameter is a Regression Target¶

Simulating Data¶

Let's first simulate some data, where the trial-by-trial parameters of the v parameter in our model are driven by a simple linear regression model.

The regression model is driven by two (random) covariates x and y, respectively with coefficients of $0.8$ and $0.3$ which are also simulated below. We set the intercept to $0.3$.

The rest of the parameters are fixed to single values as before.

In [48]:

Copied!





# Set up trial by trial parameters
v_intercept = 0.3
x = np.random.uniform(-1, 1, size=1000)
v_x = 0.8
y = np.random.uniform(-1, 1, size=1000)
v_y = 0.3
v_reg_v = v_intercept + (v_x * x) + (v_y * y)

# rest
a_reg_v = 1.5
z_reg_v = 0.5
t_reg_v = 0.1

param_dict_reg_v = dict(
    a=1.5, z=0.5, t=0.1, v=v_reg_v, v_x=v_x, v_y=v_y, v_Intercept=v_intercept, theta=0.0
)

# base dataset
dataset_reg_v = hssm.simulate_data(model="ddm", theta=param_dict_reg_v, size=1)

# Adding covariates into the datsaframe
dataset_reg_v["x"] = x
dataset_reg_v["y"] = y
# Set up trial by trial parameters
v_intercept = 0.3
x = np.random.uniform(-1, 1, size=1000)
v_x = 0.8
y = np.random.uniform(-1, 1, size=1000)
v_y = 0.3
v_reg_v = v_intercept + (v_x * x) + (v_y * y)

# rest
a_reg_v = 1.5
z_reg_v = 0.5
t_reg_v = 0.1

param_dict_reg_v = dict(
    a=1.5, z=0.5, t=0.1, v=v_reg_v, v_x=v_x, v_y=v_y, v_Intercept=v_intercept, theta=0.0
)

# base dataset
dataset_reg_v = hssm.simulate_data(model="ddm", theta=param_dict_reg_v, size=1)

# Adding covariates into the datsaframe
dataset_reg_v["x"] = x
dataset_reg_v["y"] = y

Basic Model¶

We now create the HSSM model.

Notice how we set the include argument. The include argument expects a list of dictionaries, one dictionary for each parameter to be specified via a regression model.

Four keys are expected to be set:

The name of the parameter,
Potentially a prior for each of the regression level parameters ($\beta$'s),
The regression formula
A link function.

The regression formula follows the syntax in the formulae python package (as used by the Bambi package for building Bayesian Hierarchical Regression Models.

Bambi forms the main model-construction backend of HSSM.

In [49]:

Copied!

model_reg_v_simple = hssm.HSSM(
    data=dataset_reg_v, include=[{"name": "v", "formula": "v ~ 1 + x + y"}]
)
model_reg_v_simple = hssm.HSSM(
    data=dataset_reg_v, include=[{"name": "v", "formula": "v ~ 1 + x + y"}]
)

{'t_log__': array(0.6931472, dtype=float32), 'a_log__': array(0.6931472, dtype=float32), 'z_interval__': array(0., dtype=float32), 'v_Intercept': array(0., dtype=float32), 'v_x': array(0., dtype=float32), 'v_y': array(0., dtype=float32)}

In [50]:

Copied!

model_reg_v_simple
model_reg_v_simple

Out[50]:

Hierarchical Sequential Sampling Model
Model: ddm

Response variable: rt,response
Likelihood: analytical
Observations: 1000

Parameters:

v:
    Formula: v ~ 1 + x + y
    Priors:
        v_Intercept ~ Normal(mu: 0.0, sigma: 2.503200054168701)
        v_x ~ Normal(mu: 0.0, sigma: 4.391900062561035)
        v_y ~ Normal(mu: 0.0, sigma: 4.451900005340576)
    Link: identity
    Explicit bounds: (-inf, inf)

a:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)

z:
    Prior: Uniform(lower: 0.0, upper: 1.0)
    Explicit bounds: (0.0, 1.0)

t:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)


Lapse probability: 0.05
Lapse distribution: Uniform(lower: 0.0, upper: 20.0)

`Param` class¶

As illustrated below, there is an alternative way of specifying the parameter specific data via the Param class.

In [51]:

Copied!

model_reg_v_simple_new = hssm.HSSM(
    data=dataset_reg_v, include=[hssm.Param(name="v", formula="v ~ 1 + x + y")]
)
model_reg_v_simple_new = hssm.HSSM(
    data=dataset_reg_v, include=[hssm.Param(name="v", formula="v ~ 1 + x + y")]
)

{'t_log__': array(0.6931472, dtype=float32), 'a_log__': array(0.6931472, dtype=float32), 'z_interval__': array(0., dtype=float32), 'v_Intercept': array(0., dtype=float32), 'v_x': array(0., dtype=float32), 'v_y': array(0., dtype=float32)}

In [52]:

Copied!

model_reg_v_simple_new
model_reg_v_simple_new

Out[52]:

Hierarchical Sequential Sampling Model
Model: ddm

Response variable: rt,response
Likelihood: analytical
Observations: 1000

Parameters:

v:
    Formula: v ~ 1 + x + y
    Priors:
        v_Intercept ~ Normal(mu: 0.0, sigma: 2.503200054168701)
        v_x ~ Normal(mu: 0.0, sigma: 4.391900062561035)
        v_y ~ Normal(mu: 0.0, sigma: 4.451900005340576)
    Link: identity
    Explicit bounds: (-inf, inf)

a:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)

z:
    Prior: Uniform(lower: 0.0, upper: 1.0)
    Explicit bounds: (0.0, 1.0)

t:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)


Lapse probability: 0.05
Lapse distribution: Uniform(lower: 0.0, upper: 20.0)

In [53]:

Copied!

model_reg_v_simple.graph()
model_reg_v_simple.graph()

Out[53]:

In [54]:

Copied!

print(model_reg_v_simple)
print(model_reg_v_simple)

Hierarchical Sequential Sampling Model
Model: ddm

Response variable: rt,response
Likelihood: analytical
Observations: 1000

Parameters:

v:
    Formula: v ~ 1 + x + y
    Priors:
        v_Intercept ~ Normal(mu: 0.0, sigma: 2.503200054168701)
        v_x ~ Normal(mu: 0.0, sigma: 4.391900062561035)
        v_y ~ Normal(mu: 0.0, sigma: 4.451900005340576)
    Link: identity
    Explicit bounds: (-inf, inf)

a:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)

z:
    Prior: Uniform(lower: 0.0, upper: 1.0)
    Explicit bounds: (0.0, 1.0)

t:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)


Lapse probability: 0.05
Lapse distribution: Uniform(lower: 0.0, upper: 20.0)

Custom Model¶

These were the defaults, with a little extra labor, we can e.g. customize the choice of priors for each parameter in the model.

In [55]:

Copied!





model_reg_v = hssm.HSSM(
    data=dataset_reg_v,
    include=[
        {
            "name": "v",
            "prior": {
                "Intercept": {"name": "Uniform", "lower": -3.0, "upper": 3.0},
                "x": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
                "y": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
            },
            "formula": "v ~ 1 + x + y",
            "link": "identity",
        }
    ],
)
model_reg_v = hssm.HSSM(
    data=dataset_reg_v,
    include=[
        {
            "name": "v",
            "prior": {
                "Intercept": {"name": "Uniform", "lower": -3.0, "upper": 3.0},
                "x": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
                "y": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
            },
            "formula": "v ~ 1 + x + y",
            "link": "identity",
        }
    ],
)

{'t_log__': array(0.6931472, dtype=float32), 'a_log__': array(0.6931472, dtype=float32), 'z_interval__': array(0., dtype=float32), 'v_Intercept': array(0., dtype=float32), 'v_x': array(0., dtype=float32), 'v_y': array(0., dtype=float32)}

In [56]:

Copied!

model_reg_v
model_reg_v

Out[56]:

Hierarchical Sequential Sampling Model
Model: ddm

Response variable: rt,response
Likelihood: analytical
Observations: 1000

Parameters:

v:
    Formula: v ~ 1 + x + y
    Priors:
        v_Intercept ~ Normal(mu: 0.0, sigma: 2.503200054168701)
        v_x ~ Normal(mu: 0.0, sigma: 4.391900062561035)
        v_y ~ Normal(mu: 0.0, sigma: 4.451900005340576)
    Link: identity
    Explicit bounds: (-inf, inf)

a:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)

z:
    Prior: Uniform(lower: 0.0, upper: 1.0)
    Explicit bounds: (0.0, 1.0)

t:
    Prior: HalfNormal(sigma: 2.0)
    Explicit bounds: (0.0, inf)


Lapse probability: 0.05
Lapse distribution: Uniform(lower: 0.0, upper: 20.0)

Notice how v is now set as a regression.

In [57]:

Copied!

infer_data_reg_v = model_reg_v.sample(
    sampler="nuts_numpyro", chains=1, cores=1, draws=500, tune=500
)
infer_data_reg_v = model_reg_v.sample(
    sampler="nuts_numpyro", chains=1, cores=1, draws=500, tune=500
)

Using default initvals.

sample: 100%|██████████| 1000/1000 [00:06<00:00, 158.78it/s, 7 steps of size 5.85e-01. acc. prob=0.90]
Only one chain was sampled, this makes it impossible to run some convergence checks

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x2f3c7b350>
PERFORMING PREDICTION

Output()

In [59]:

Copied!

# az.plot_forest(model_reg_v.traces)
# az.plot_forest(model_reg_v.traces)

In [60]:

Copied!





az.plot_trace(
    model_reg_v.traces,
    var_names=["~v"],
    lines=[(key_, {}, param_dict_reg_v[key_]) for key_ in param_dict_reg_v],
)
az.plot_trace(
    model_reg_v.traces,
    var_names=["~v"],
    lines=[(key_, {}, param_dict_reg_v[key_]) for key_ in param_dict_reg_v],
)

Out[60]:

array([[<Axes: title={'center': 'v_Intercept'}>,
        <Axes: title={'center': 'v_Intercept'}>],
       [<Axes: title={'center': 'a'}>, <Axes: title={'center': 'a'}>],
       [<Axes: title={'center': 'v_x'}>, <Axes: title={'center': 'v_x'}>],
       [<Axes: title={'center': 't'}>, <Axes: title={'center': 't'}>],
       [<Axes: title={'center': 'z'}>, <Axes: title={'center': 'z'}>],
       [<Axes: title={'center': 'v_y'}>, <Axes: title={'center': 'v_y'}>]],
      dtype=object)

In [61]:

Copied!





az.plot_trace(
    model_reg_v.traces,
    var_names=["~v"],
    lines=[(key_, {}, param_dict_reg_v[key_]) for key_ in param_dict_reg_v],
)
plt.tight_layout()
az.plot_trace(
    model_reg_v.traces,
    var_names=["~v"],
    lines=[(key_, {}, param_dict_reg_v[key_]) for key_ in param_dict_reg_v],
)
plt.tight_layout()

In [62]:

Copied!

# Looks like parameter recovery was successful
az.summary(model_reg_v.traces, var_names=["~v"])
# Looks like parameter recovery was successful
az.summary(model_reg_v.traces, var_names=["~v"])

arviz - WARNING - Shape validation failed: input_shape: (1, 500), minimum_shape: (chains=2, draws=4)

Out[62]:

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
v_Intercept	0.311	0.034	0.246	0.373	0.002	0.001	351.0	302.0	NaN
a	1.498	0.030	1.442	1.551	0.001	0.001	438.0	455.0	NaN
v_x	0.792	0.048	0.705	0.880	0.002	0.001	587.0	370.0	NaN
t	0.089	0.020	0.047	0.123	0.001	0.001	345.0	299.0	NaN
z	0.495	0.013	0.471	0.518	0.001	0.000	372.0	396.0	NaN
v_y	0.270	0.046	0.185	0.349	0.002	0.001	595.0	390.0	NaN

Case 2: One parameter is a Regression (LAN)¶

We can do the same thing with the angle model.

Note:

Our dataset was generated from the basic DDM here, so since the DDM assumes stable bounds, we expect the theta (angle of linear collapse) parameter to be recovered as close to $0$.

In [63]:

Copied!





model_reg_v_angle = hssm.HSSM(
    data=dataset_reg_v,
    model="angle",
    include=[
        {
            "name": "v",
            "prior": {
                "Intercept": {
                    "name": "Uniform",
                    "lower": -3.0,
                    "upper": 3.0,
                },
                "x": {
                    "name": "Uniform",
                    "lower": -1.0,
                    "upper": 1.0,
                },
                "y": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
            },
            "formula": "v ~ 1 + x + y",
            "link": "identity",
        }
    ],
)
model_reg_v_angle = hssm.HSSM(
    data=dataset_reg_v,
    model="angle",
    include=[
        {
            "name": "v",
            "prior": {
                "Intercept": {
                    "name": "Uniform",
                    "lower": -3.0,
                    "upper": 3.0,
                },
                "x": {
                    "name": "Uniform",
                    "lower": -1.0,
                    "upper": 1.0,
                },
                "y": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
            },
            "formula": "v ~ 1 + x + y",
            "link": "identity",
        }
    ],
)

{'a_interval__': array(-8.940697e-08, dtype=float32), 't_interval__': array(-5.9604645e-08, dtype=float32), 'z_interval__': array(1.1920929e-07, dtype=float32), 'theta_interval__': array(0., dtype=float32), 'v_Intercept': array(0., dtype=float32), 'v_x': array(0., dtype=float32), 'v_y': array(0., dtype=float32)}

In [64]:

Copied!

model_reg_v_angle.graph()
model_reg_v_angle.graph()

Out[64]:

In [65]:

Copied!

trace_reg_v_angle = model_reg_v_angle.sample(
    sampler="nuts_numpyro", chains=1, cores=1, draws=1000, tune=500
)
trace_reg_v_angle = model_reg_v_angle.sample(
    sampler="nuts_numpyro", chains=1, cores=1, draws=1000, tune=500
)

Using default initvals.

sample: 100%|██████████| 1500/1500 [00:20<00:00, 73.76it/s, 7 steps of size 2.33e-01. acc. prob=0.96]  
Only one chain was sampled, this makes it impossible to run some convergence checks

Output()

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x2b90b8450>
PERFORMING PREDICTION

In [66]:

Copied!





az.plot_trace(
    model_reg_v_angle.traces,
    var_names=["~v"],
    lines=[(key_, {}, param_dict_reg_v[key_]) for key_ in param_dict_reg_v],
)
plt.tight_layout()
az.plot_trace(
    model_reg_v_angle.traces,
    var_names=["~v"],
    lines=[(key_, {}, param_dict_reg_v[key_]) for key_ in param_dict_reg_v],
)
plt.tight_layout()

Great! theta is recovered correctly, on top of that, we have reasonable recovery for all other parameters!

Case 3: Multiple Parameters are Regression Targets (LAN)¶

Let's get a bit more ambitious. We may, for example, want to try a regression on a few of our basic model parameters at once. Below we show an example where we model both the a and the v parameters with a regression.

NOTE:

In our dataset of this section, only v is actually driven by a trial-by-trial regression, so we expect the regression coefficients for a to hover around $0$ in our posterior.

In [67]:

Copied!





# Instantiate our hssm model
from copy import deepcopy

param_dict_reg_v_a = deepcopy(param_dict_reg_v)
param_dict_reg_v_a["a_Intercept"] = param_dict_reg_v_a["a"]
param_dict_reg_v_a["a_x"] = 0
param_dict_reg_v_a["a_y"] = 0

hssm_reg_v_a_angle = hssm.HSSM(
    data=dataset_reg_v,
    model="angle",
    include=[
        {
            "name": "v",
            "prior": {
                "Intercept": {"name": "Uniform", "lower": -3.0, "upper": 3.0},
                "x": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
                "y": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
            },
            "formula": "v ~ 1 + x + y",
        },
        {
            "name": "a",
            "prior": {
                "Intercept": {"name": "Uniform", "lower": 0.5, "upper": 3.0},
                "x": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
                "y": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
            },
            "formula": "a ~ 1 + x + y",
        },
    ],
)
# Instantiate our hssm model
from copy import deepcopy

param_dict_reg_v_a = deepcopy(param_dict_reg_v)
param_dict_reg_v_a["a_Intercept"] = param_dict_reg_v_a["a"]
param_dict_reg_v_a["a_x"] = 0
param_dict_reg_v_a["a_y"] = 0

hssm_reg_v_a_angle = hssm.HSSM(
    data=dataset_reg_v,
    model="angle",
    include=[
        {
            "name": "v",
            "prior": {
                "Intercept": {"name": "Uniform", "lower": -3.0, "upper": 3.0},
                "x": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
                "y": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
            },
            "formula": "v ~ 1 + x + y",
        },
        {
            "name": "a",
            "prior": {
                "Intercept": {"name": "Uniform", "lower": 0.5, "upper": 3.0},
                "x": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
                "y": {"name": "Uniform", "lower": -1.0, "upper": 1.0},
            },
            "formula": "a ~ 1 + x + y",
        },
    ],
)

{'t_interval__': array(-5.9604645e-08, dtype=float32), 'z_interval__': array(1.1920929e-07, dtype=float32), 'theta_interval__': array(0., dtype=float32), 'v_Intercept': array(0., dtype=float32), 'v_x': array(0., dtype=float32), 'v_y': array(0., dtype=float32), 'a_Intercept_interval__': array(0., dtype=float32), 'a_x_interval__': array(0., dtype=float32), 'a_y_interval__': array(0., dtype=float32)}

In [68]:

Copied!

hssm_reg_v_a_angle
hssm_reg_v_a_angle

Out[68]:

Hierarchical Sequential Sampling Model
Model: angle

Response variable: rt,response
Likelihood: approx_differentiable
Observations: 1000

Parameters:

v:
    Formula: v ~ 1 + x + y
    Priors:
        v_Intercept ~ Normal(mu: 0.0, sigma: 2.503200054168701)
        v_x ~ Normal(mu: 0.0, sigma: 4.391900062561035)
        v_y ~ Normal(mu: 0.0, sigma: 4.451900005340576)
    Link: identity
    Explicit bounds: (-3.0, 3.0)

a:
    Formula: a ~ 1 + x + y
    Priors:
        a_Intercept ~ Uniform(lower: 0.5, upper: 3.0)
        a_x ~ Uniform(lower: -1.0, upper: 1.0)
        a_y ~ Uniform(lower: -1.0, upper: 1.0)
    Link: identity
    Explicit bounds: (0.3, 3.0)

z:
    Prior: Uniform(lower: 0.10000000149011612, upper: 0.8999999761581421)
    Explicit bounds: (0.1, 0.9)

t:
    Prior: Uniform(lower: 0.0010000000474974513, upper: 2.0)
    Explicit bounds: (0.001, 2.0)

theta:
    Prior: Uniform(lower: -0.10000000149011612, upper: 1.2999999523162842)
    Explicit bounds: (-0.1, 1.3)


Lapse probability: 0.05
Lapse distribution: Uniform(lower: 0.0, upper: 20.0)

In [69]:

Copied!

hssm_reg_v_a_angle.graph()
hssm_reg_v_a_angle.graph()

Out[69]:

In [70]:

Copied!

infer_data_reg_v_a = hssm_reg_v_a_angle.sample(
    sampler="nuts_numpyro", chains=2, cores=1, draws=1000, tune=1000
)
infer_data_reg_v_a = hssm_reg_v_a_angle.sample(
    sampler="nuts_numpyro", chains=2, cores=1, draws=1000, tune=1000
)

Using default initvals.

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

We recommend running at least 4 chains for robust computation of convergence diagnostics

Output()

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x314ead810>
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x314ead590>
PERFORMING PREDICTION

In [71]:

Copied!

az.summary(
    infer_data_reg_v_a, var_names=["~a", "~v"]
)  # , var_names=["~rt,response_a"])
az.summary(
    infer_data_reg_v_a, var_names=["~a", "~v"]
)  # , var_names=["~rt,response_a"])

Out[71]:

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
v_Intercept	0.299	0.033	0.241	0.361	0.001	0.001	1408.0	1381.0	1.0
v_x	0.795	0.047	0.711	0.885	0.001	0.001	2000.0	1399.0	1.0
a_x	0.045	0.044	-0.032	0.132	0.001	0.001	2065.0	1444.0	1.0
t	0.055	0.025	0.006	0.098	0.001	0.001	901.0	801.0	1.0
z	0.504	0.012	0.482	0.528	0.000	0.000	1237.0	1251.0	1.0
v_y	0.270	0.043	0.190	0.351	0.001	0.001	2388.0	1276.0	1.0
a_Intercept	1.594	0.050	1.501	1.689	0.002	0.001	918.0	1164.0	1.0
a_y	0.026	0.039	-0.039	0.106	0.001	0.001	2160.0	1503.0	1.0
theta	0.059	0.020	0.019	0.095	0.001	0.000	1060.0	954.0	1.0

In [72]:

Copied!





az.plot_trace(
    hssm_reg_v_a_angle.traces,
    var_names=["~v", "~a"],
    lines=[(key_, {}, param_dict_reg_v_a[key_]) for key_ in param_dict_reg_v_a],
)
plt.tight_layout()
az.plot_trace(
    hssm_reg_v_a_angle.traces,
    var_names=["~v", "~a"],
    lines=[(key_, {}, param_dict_reg_v_a[key_]) for key_ in param_dict_reg_v_a],
)
plt.tight_layout()

We successfully recover our regression betas for a! Moreover, no warning signs concerning our chains.

Case 4: Categorical covariates¶

In [73]:

Copied!





# Set up trial by trial parameters
x = np.random.choice(4, size=1000).astype(int)
x_offset = np.array([0, 1, -0.5, 0.75])

y = np.random.uniform(-1, 1, size=1000)
v_y = 0.3
v_reg_v = 0 + (v_y * y) + x_offset[x]

# rest
a_reg_v = 1.5
z_reg_v = 0.5
t_reg_v = 0.1

# base dataset
dataset_reg_v_cat = hssm.simulate_data(
    model="ddm", theta=dict(v=v_reg_v, a=a_reg_v, z=z_reg_v, t=t_reg_v), size=1
)

# Adding covariates into the datsaframe
dataset_reg_v_cat["x"] = x
dataset_reg_v_cat["y"] = y
# Set up trial by trial parameters
x = np.random.choice(4, size=1000).astype(int)
x_offset = np.array([0, 1, -0.5, 0.75])

y = np.random.uniform(-1, 1, size=1000)
v_y = 0.3
v_reg_v = 0 + (v_y * y) + x_offset[x]

# rest
a_reg_v = 1.5
z_reg_v = 0.5
t_reg_v = 0.1

# base dataset
dataset_reg_v_cat = hssm.simulate_data(
    model="ddm", theta=dict(v=v_reg_v, a=a_reg_v, z=z_reg_v, t=t_reg_v), size=1
)

# Adding covariates into the datsaframe
dataset_reg_v_cat["x"] = x
dataset_reg_v_cat["y"] = y

In [74]:

Copied!





model_reg_v_cat = hssm.HSSM(
    data=dataset_reg_v_cat,
    model="angle",
    include=[
        {
            "name": "v",
            "formula": "v ~ 0 + C(x) + y",
            "link": "identity",
        }
    ],
)
model_reg_v_cat = hssm.HSSM(
    data=dataset_reg_v_cat,
    model="angle",
    include=[
        {
            "name": "v",
            "formula": "v ~ 0 + C(x) + y",
            "link": "identity",
        }
    ],
)

{'a_interval__': array(-8.940697e-08, dtype=float32), 't_interval__': array(-5.9604645e-08, dtype=float32), 'z_interval__': array(1.1920929e-07, dtype=float32), 'theta_interval__': array(0., dtype=float32), 'v_C(x)': array([0., 0., 0., 0.], dtype=float32), 'v_y': array(0., dtype=float32)}

In [75]:

Copied!

model_reg_v_cat.graph()
model_reg_v_cat.graph()

Out[75]:

In [76]:

Copied!

infer_data_reg_v_cat = model_reg_v_cat.sample(
    sampler="nuts_numpyro", chains=2, cores=1, draws=1000, tune=500
)
infer_data_reg_v_cat = model_reg_v_cat.sample(
    sampler="nuts_numpyro", chains=2, cores=1, draws=1000, tune=500
)

Using default initvals.

  0%|          | 0/1500 [00:00<?, ?it/s]

  0%|          | 0/1500 [00:00<?, ?it/s]

We recommend running at least 4 chains for robust computation of convergence diagnostics

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x2f154f110>
PERFORMING PREDICTION

Output()

In [77]:

Copied!

az.plot_forest(infer_data_reg_v_cat, var_names=["~v"])
az.plot_forest(infer_data_reg_v_cat, var_names=["~v"])

Out[77]:

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

Hierarchical Inference¶

Let's try to fit a hierarchical model now. We will simulate a dataset with $15$ participants, with $200$ observations / trials for each participant.

We define a group mean mean_v and a group standard deviation sd_v for the intercept parameter of the regression on v, which we sample from a corresponding normal distribution for each participant.

Simulate Data¶

In [78]:

Copied!





# Make some hierarchical data

n_participants = 15  # number of participants
n_trials = 200  # number of trials per participant

sd_v = 0.5  # sd for v-intercept
mean_v = 0.5  # mean for v-intercept

data_list = []
for i in range(n_participants):
    # Make parameters for participant i
    v_intercept_hier = np.random.normal(mean_v, sd_v, size=1)
    x = np.random.uniform(-1, 1, size=n_trials)
    v_x_hier = 0.8
    y = np.random.uniform(-1, 1, size=n_trials)
    v_y_hier = 0.3
    v_hier = v_intercept_hier + (v_x_hier * x) + (v_y_hier * y)

    a_hier = 1.5
    t_hier = 0.5
    z_hier = 0.5

    # true_values = np.column_stack(
    #     [v, np.repeat([[1.5, 0.5, 0.5, 0.0]], axis=0, repeats=n_trials)]
    # )

    data_tmp = hssm.simulate_data(
        model="ddm", theta=dict(v=v_hier, a=a_hier, z=z_hier, t=t_hier), size=1
    )
    data_tmp["participant_id"] = i
    data_tmp["x"] = x
    data_tmp["y"] = y

    data_list.append(data_tmp)

# Make single dataframe out of participant-wise datasets
dataset_reg_v_hier = pd.concat(data_list)
dataset_reg_v_hier
# Make some hierarchical data

n_participants = 15  # number of participants
n_trials = 200  # number of trials per participant

sd_v = 0.5  # sd for v-intercept
mean_v = 0.5  # mean for v-intercept

data_list = []
for i in range(n_participants):
    # Make parameters for participant i
    v_intercept_hier = np.random.normal(mean_v, sd_v, size=1)
    x = np.random.uniform(-1, 1, size=n_trials)
    v_x_hier = 0.8
    y = np.random.uniform(-1, 1, size=n_trials)
    v_y_hier = 0.3
    v_hier = v_intercept_hier + (v_x_hier * x) + (v_y_hier * y)

    a_hier = 1.5
    t_hier = 0.5
    z_hier = 0.5

    # true_values = np.column_stack(
    #     [v, np.repeat([[1.5, 0.5, 0.5, 0.0]], axis=0, repeats=n_trials)]
    # )

    data_tmp = hssm.simulate_data(
        model="ddm", theta=dict(v=v_hier, a=a_hier, z=z_hier, t=t_hier), size=1
    )
    data_tmp["participant_id"] = i
    data_tmp["x"] = x
    data_tmp["y"] = y

    data_list.append(data_tmp)

# Make single dataframe out of participant-wise datasets
dataset_reg_v_hier = pd.concat(data_list)
dataset_reg_v_hier

Out[78]:

	rt	response	participant_id	x	y
0	2.397503	1.0	0	-0.535751	0.573336
1	4.983025	1.0	0	-0.158811	0.024659
2	2.092753	1.0	0	-0.556658	0.021410
3	1.534563	1.0	0	-0.610495	-0.315694
4	1.945778	1.0	0	0.499722	0.272538
...	...	...	...	...	...
195	2.887140	1.0	14	-0.918860	0.234293
196	2.688891	1.0	14	-0.899047	-0.707518
197	1.102728	1.0	14	0.282337	0.789865
198	2.264880	1.0	14	0.152510	-0.697267
199	1.296382	1.0	14	-0.340144	0.562373

3000 rows × 5 columns

We can now define our HSSM model.

We specify the regression as v ~ 1 + (1|participant_id) + x + y.

(1|participant_id) tells the model to create a participant-wise offset for the intercept parameter. The rest of the regression $\beta$'s is fit globally.

As an R user you may recognize this syntax from the lmer package.

Our Bambi backend is essentially a Bayesian version of lmer, quite like the BRMS package in R, which operates on top of STAN.

As a previous HDDM user, you may recognize that now proper mixed-effect models are viable!

You should be able to handle between and within participant effects naturally now!

Basic Hierarchical Model¶

In [79]:

Copied!





model_reg_v_angle_hier = hssm.HSSM(
    data=dataset_reg_v_hier,
    model="angle",
    noncentered=True,
    include=[
        {
            "name": "v",
            "prior": {
                "Intercept": {
                    "name": "Normal",
                    "mu": 0.0,
                    "sigma": 0.5,
                },
                "x": {"name": "Normal", "mu": 0.0, "sigma": 0.5},
                "y": {"name": "Normal", "mu": 0.0, "sigma": 0.5},
            },
            "formula": "v ~ 1 + (1|participant_id) + x + y",
            "link": "identity",
        }
    ],
)
model_reg_v_angle_hier = hssm.HSSM(
    data=dataset_reg_v_hier,
    model="angle",
    noncentered=True,
    include=[
        {
            "name": "v",
            "prior": {
                "Intercept": {
                    "name": "Normal",
                    "mu": 0.0,
                    "sigma": 0.5,
                },
                "x": {"name": "Normal", "mu": 0.0, "sigma": 0.5},
                "y": {"name": "Normal", "mu": 0.0, "sigma": 0.5},
            },
            "formula": "v ~ 1 + (1|participant_id) + x + y",
            "link": "identity",
        }
    ],
)

{'a_interval__': array(-8.940697e-08, dtype=float32), 't_interval__': array(-5.9604645e-08, dtype=float32), 'z_interval__': array(1.1920929e-07, dtype=float32), 'theta_interval__': array(0., dtype=float32), 'v_Intercept': array(0., dtype=float32), 'v_x': array(0., dtype=float32), 'v_y': array(0., dtype=float32), 'v_1|participant_id_sigma_log__': array(0.91670346, dtype=float32), 'v_1|participant_id_offset': array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
      dtype=float32)}

In [80]:

Copied!

model_reg_v_angle_hier.graph()
model_reg_v_angle_hier.graph()

Out[80]:

Let's look at the posteriors!

In [82]:

Copied!

az.plot_forest(model_reg_v_angle_hier.traces, var_names=["~v", "~a"], combined=False)
az.plot_forest(model_reg_v_angle_hier.traces, var_names=["~v", "~a"], combined=False)

Out[82]:

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

Model Comparison¶

Fitting single models is all well and good. We are however, often interested in comparing how well a few different models account for the same data.

Through ArviZ, we have out of the box access to modern Bayesian Model Comparison. We will keep it simple here, just to illustrate the basic idea.

Scenario¶

The following scenario is explored.

First we generate data from a ddm model with fixed parameters, specifically we set the a parameter to $1.5$.

We then define two HSSM models:

A model which allows fitting all but the a parameter, which is fixed to $1.0$ (wrong)
A model which allows fitting all but the a parameter, which is fixed to $1.5$ (correct)

We then use the ArviZ's compare() function, to perform model comparison via elpd_loo.

Data Simulation¶

In [83]:

Copied!





# Parameters
param_dict_mod_comp = dict(v=0.5, a=1.5, z=0.5, t=0.2)

# Simulation
dataset_model_comp = hssm.simulate_data(
    model="ddm", theta=param_dict_mod_comp, size=500
)

print(dataset_model_comp)
# Parameters
param_dict_mod_comp = dict(v=0.5, a=1.5, z=0.5, t=0.2)

# Simulation
dataset_model_comp = hssm.simulate_data(
    model="ddm", theta=param_dict_mod_comp, size=500
)

print(dataset_model_comp)

           rt  response
0    0.921197       1.0
1    0.943467       1.0
2    1.156752      -1.0
3    1.330700       1.0
4    3.722521       1.0
..        ...       ...
495  2.176493       1.0
496  2.545375       1.0
497  5.816162       1.0
498  0.639278       1.0
499  3.823134      -1.0

[500 rows x 2 columns]

Defining the Models¶

In [84]:

Copied!





# 'wrong' model
model_model_comp_1 = hssm.HSSM(
    data=dataset_model_comp,
    model="angle",
    a=1.0,
)
# 'wrong' model
model_model_comp_1 = hssm.HSSM(
    data=dataset_model_comp,
    model="angle",
    a=1.0,
)

{'t_interval__': array(-5.9604645e-08, dtype=float32), 'z_interval__': array(1.1920929e-07, dtype=float32), 'theta_interval__': array(0., dtype=float32), 'v': array(0., dtype=float32)}

In [85]:

Copied!





# 'correct' model
model_model_comp_2 = hssm.HSSM(
    data=dataset_model_comp,
    model="angle",
    a=1.5,
)
# 'correct' model
model_model_comp_2 = hssm.HSSM(
    data=dataset_model_comp,
    model="angle",
    a=1.5,
)

{'t_interval__': array(-5.9604645e-08, dtype=float32), 'z_interval__': array(1.1920929e-07, dtype=float32), 'theta_interval__': array(0., dtype=float32), 'v': array(0., dtype=float32)}

In [86]:

Copied!





# 'wrong' model ddm
model_model_comp_3 = hssm.HSSM(
    data=dataset_model_comp,
    model="ddm",
    a=1.0,
)
# 'wrong' model ddm
model_model_comp_3 = hssm.HSSM(
    data=dataset_model_comp,
    model="ddm",
    a=1.0,
)

{'t_log__': array(0.6931472, dtype=float32), 'z_interval__': array(0., dtype=float32), 'v': array(0., dtype=float32)}

In [87]:

Copied!





infer_data_model_comp_1 = model_model_comp_1.sample(
    sampler="nuts_numpyro",
    cores=1,
    chains=2,
    draws=1000,
    tune=1000,
    idata_kwargs=dict(
        log_likelihood=True
    ),  # model comparison metrics usually need this!
)
infer_data_model_comp_1 = model_model_comp_1.sample(
    sampler="nuts_numpyro",
    cores=1,
    chains=2,
    draws=1000,
    tune=1000,
    idata_kwargs=dict(
        log_likelihood=True
    ),  # model comparison metrics usually need this!
)

Using default initvals.

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

We recommend running at least 4 chains for robust computation of convergence diagnostics

Output()

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x314daa890>
PERFORMING PREDICTION

In [88]:

Copied!





infer_data_model_comp_2 = model_model_comp_2.sample(
    sampler="nuts_numpyro",
    cores=1,
    chains=2,
    draws=1000,
    tune=1000,
    idata_kwargs=dict(
        log_likelihood=True
    ),  # model comparison metrics usually need this!
)
infer_data_model_comp_2 = model_model_comp_2.sample(
    sampler="nuts_numpyro",
    cores=1,
    chains=2,
    draws=1000,
    tune=1000,
    idata_kwargs=dict(
        log_likelihood=True
    ),  # model comparison metrics usually need this!
)

Using default initvals.

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

We recommend running at least 4 chains for robust computation of convergence diagnostics

Output()

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x3155eaad0>
PERFORMING PREDICTION

In [89]:

Copied!





infer_data_model_comp_3 = model_model_comp_3.sample(
    sampler="nuts_numpyro",
    cores=1,
    chains=2,
    draws=1000,
    tune=1000,
    idata_kwargs=dict(
        log_likelihood=True
    ),  # model comparison metrics usually need this!
)
infer_data_model_comp_3 = model_model_comp_3.sample(
    sampler="nuts_numpyro",
    cores=1,
    chains=2,
    draws=1000,
    tune=1000,
    idata_kwargs=dict(
        log_likelihood=True
    ),  # model comparison metrics usually need this!
)

Using default initvals.

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

There were 96 divergences after tuning. Increase `target_accept` or reparameterize.
We recommend running at least 4 chains for robust computation of convergence diagnostics

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x31520b250>
PERFORMING PREDICTION

Output()

Compare¶

In [90]:

Copied!





compare_data = az.compare(
    {
        "a_fixed_1(wrong)": model_model_comp_1.traces,
        "a_fixed_1.5(correct)": model_model_comp_2.traces,
        "a_fixed_1_ddm(wrong)": model_model_comp_3.traces,
    }
)

compare_data
compare_data = az.compare(
    {
        "a_fixed_1(wrong)": model_model_comp_1.traces,
        "a_fixed_1.5(correct)": model_model_comp_2.traces,
        "a_fixed_1_ddm(wrong)": model_model_comp_3.traces,
    }
)

compare_data

Out[90]:

	rank	elpd_loo	p_loo	elpd_diff	weight	se	dse	warning	scale
a_fixed_1.5(correct)	0	-1016.852568	3.358483	0.000000	1.000000e+00	24.833365	0.000000	False	log
a_fixed_1(wrong)	1	-1086.224081	3.446915	69.371513	7.475381e-11	30.606928	10.840982	False	log
a_fixed_1_ddm(wrong)	2	-1169.706585	3.872999	152.854017	0.000000e+00	35.799180	17.050865	False	log

Notice how the posterior weight on the correct model is close to (or equal to ) $1$ here. In other words model comparison points us to the correct model with a very high degree of certainty here!

We can also use the .plot_compare() function to illustrate the model comparison visually.

In [91]:

Copied!

az.plot_compare(compare_data)
az.plot_compare(compare_data)

Out[91]:

<Axes: title={'center': 'Model comparison\nhigher is better'}, xlabel='elpd_loo (log)', ylabel='ranked models'>

Using the forest plot we can take a look at what goes wrong for the "wrong" model.

To make up for the mistplaced setting of the a parameter, the posterior seems to compensate by mis-estimating the other parameters.

In [92]:

Copied!





az.plot_forest(
    [model_model_comp_1.traces, model_model_comp_2.traces, model_model_comp_3.traces],
    model_names=["a_fixed_1(wrong)", "a_fixed_1.5(correct)", "a_fixed_1(wrong)_ddm"],
)
az.plot_forest(
    [model_model_comp_1.traces, model_model_comp_2.traces, model_model_comp_3.traces],
    model_names=["a_fixed_1(wrong)", "a_fixed_1.5(correct)", "a_fixed_1(wrong)_ddm"],
)

Out[92]:

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

Closer look!¶

We have seen a few examples of HSSM models at this point. Add a model via a string, maybe toy a bit with with the priors and set regression functions for a given parameter. Turn it hierarchical... Here we begin to peak a bit under the hood.

After all, we want to encourage you to contribute models to the package yourself.

Let's remind ourself of the model_config dictionaries that define model properties for us. Again let's start with the DDM.

In [93]:

Copied!

hssm.config.default_model_config["ddm"].keys()
hssm.config.default_model_config["ddm"].keys()

Out[93]:

dict_keys(['response', 'list_params', 'description', 'likelihoods'])

The dictionary has a few high level keys.

response
list_params
description
likelihoods

Let us take a look at the available likelihoods:

In [94]:

Copied!

hssm.config.default_model_config["ddm"]["likelihoods"]
hssm.config.default_model_config["ddm"]["likelihoods"]

Out[94]:

{'analytical': {'loglik': <function hssm.likelihoods.analytical.logp_ddm(data: numpy.ndarray, v: float, a: float, z: float, t: float, err: float = 1e-15, k_terms: int = 20, epsilon: float = 1e-15) -> numpy.ndarray>,
  'backend': None,
  'bounds': {'v': (-inf, inf),
   'a': (0.0, inf),
   'z': (0.0, 1.0),
   't': (0.0, inf)},
  'default_priors': {'t': {'name': 'HalfNormal', 'sigma': 2.0}},
  'extra_fields': None},
 'approx_differentiable': {'loglik': 'ddm.onnx',
  'backend': 'jax',
  'default_priors': {'t': {'name': 'HalfNormal', 'sigma': 2.0}},
  'bounds': {'v': (-3.0, 3.0),
   'a': (0.3, 2.5),
   'z': (0.0, 1.0),
   't': (0.0, 2.0)},
  'extra_fields': None},
 'blackbox': {'loglik': <function hssm.likelihoods.blackbox.hddm_to_hssm.<locals>.outer(data: numpy.ndarray, *args, **kwargs)>,
  'backend': None,
  'bounds': {'v': (-inf, inf),
   'a': (0.0, inf),
   'z': (0.0, 1.0),
   't': (0.0, inf)},
  'default_priors': {'t': {'name': 'HalfNormal', 'sigma': 2.0}},
  'extra_fields': None}}

For the DDM we have available all three types of likelihoods that HSSM deals with:

analytical
approx_differentiable
blackbox

Let's expand the dictionary contents more:

In [95]:

Copied!

hssm.config.default_model_config["ddm"]["likelihoods"]["analytical"]
hssm.config.default_model_config["ddm"]["likelihoods"]["analytical"]

Out[95]:

{'loglik': <function hssm.likelihoods.analytical.logp_ddm(data: numpy.ndarray, v: float, a: float, z: float, t: float, err: float = 1e-15, k_terms: int = 20, epsilon: float = 1e-15) -> numpy.ndarray>,
 'backend': None,
 'bounds': {'v': (-inf, inf),
  'a': (0.0, inf),
  'z': (0.0, 1.0),
  't': (0.0, inf)},
 'default_priors': {'t': {'name': 'HalfNormal', 'sigma': 2.0}},
 'extra_fields': None}

We see three properties (key) in this dictionary, of which two are essential:

The loglik field, which points to the likelihood function
The backend field, which can be either None (defaulting to pytensor for analytical likelihoods), jax or pytensor
The bounds field, which specifies bounds on a subset of the model parameters
The default_priors field, which specifies parameter wise priors

If you provide bounds for a parameter, but no default_priors, a Uniform prior that respects the specified bounds will be applied.

Next, let's look at the approx_differentiable part. The likelihood in this part is based on a LAN which was available in HDDM through the LAN extension.

In [96]:

Copied!

hssm.config.default_model_config["ddm"]["likelihoods"]["approx_differentiable"]
hssm.config.default_model_config["ddm"]["likelihoods"]["approx_differentiable"]

Out[96]:

{'loglik': 'ddm.onnx',
 'backend': 'jax',
 'default_priors': {'t': {'name': 'HalfNormal', 'sigma': 2.0}},
 'bounds': {'v': (-3.0, 3.0),
  'a': (0.3, 2.5),
  'z': (0.0, 1.0),
  't': (0.0, 2.0)},
 'extra_fields': None}

We see that the loglik field is now a string that points to a .onnx file. Onnx is a meta framework for Neural Network specification, that allows translation between deep learning Frameworks. This is the preferred format for the neural networks we store in our model reservoir on HuggingFace.

Moreover notice that we now have a backend field. We allow for two primary backends in the approx_differentiable field.

pytensor
jax

The jax backend assumes that your likelihood is described as a jax function, the pytensor backend assumes that your likelihood is described as a pytensor function. Ok not that surprising...

We won't dwell on this here, however the key idea is to provide users with a large degree of flexibility in describing their likelihood functions and moreover to allow targeted optimization towards MCMC sampler types that PyMC allows us to access.

You can find a dedicated tutorial in the documentation, which describes the different likelihoods in much more detail.

Instead, let's take a quick look at how these newfound insights can be used for custom model definition.

In [97]:

Copied!





hssm_alternative_model = hssm.HSSM(
    data=dataset,
    model="ddm",
    loglik_kind="approx_differentiable",
)
hssm_alternative_model = hssm.HSSM(
    data=dataset,
    model="ddm",
    loglik_kind="approx_differentiable",
)

{'t_log__': array(0.6931472, dtype=float32), 'a_interval__': array(-1.1175871e-07, dtype=float32), 'z_interval__': array(0., dtype=float32), 'v': array(0., dtype=float32)}

In [98]:

Copied!

hssm_alternative_model.loglik_kind
hssm_alternative_model.loglik_kind

Out[98]:

'approx_differentiable'

In this case we actually built the model class with an approx_differentiable LAN likelihood, instead of the default analytical likelihood we used in the beginning of the tutorial. The assumed generative model remains the ddm however!

In [100]:

Copied!

az.plot_forest(hssm_alternative_model.traces)
az.plot_forest(hssm_alternative_model.traces)

Out[100]:

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

We can take this further and specify a completely custom likelihood. See the dedicated tutorial for more examples!

We will see one specific example below to illustrate another type of likelihood function we have available for model building in HSSM, the Blackbox likelihood.

'Blackbox' Likelihoods¶

What is a Blackbox Likelihood Function?¶

A Blackbox Likelihood Function is essentially any Python callable (function) that provides trial by trial likelihoods for your model of interest. What kind of computations are performed in this Python function is completely arbitrary.

E.g. you could built a function that performs forward simulation from you model, constructs are kernel-density estimate for the resulting likelihood functions and evaluates your datapoints on this ad-hoc generated approximate likelihood.

What I just described is a once state-of-the-art method of performing simulation based inference on Sequential Sampling models, a precursor to LANs if you will.

We will do something simpler to keep it short and sweet, but really... the possibilities are endless!

Simulating simple dataset from the DDM¶

As always, let's begin by generating some simple dataset.

In [101]:

Copied!

# Set parameters
param_dict_blackbox = dict(v=0.5, a=1.5, z=0.5, t=0.5)

# Simulate
dataset_blackbox = hssm.simulate_data(model="ddm", theta=param_dict_blackbox, size=1000)
# Set parameters
param_dict_blackbox = dict(v=0.5, a=1.5, z=0.5, t=0.5)

# Simulate
dataset_blackbox = hssm.simulate_data(model="ddm", theta=param_dict_blackbox, size=1000)

Define the likelihood¶

Now the fun part... we simply define a Python function my_blackbox_loglik which takes in our data as well as a bunch of model parameters (in our case the familiar v,a, z, t from the DDM).

The function then does some arbitrary computation inside (in our case e.g. we pass the data and parameters to the DDM log-likelihood from our predecessor package HDDM).

The important part is that inside my_blackbox_loglik anything can happen. We happen to call a little custom function that defines the likelihood of a DDM.

Fun fact: It is de-facto the likelihood which is called by HDDM.

In [102]:

Copied!





def my_blackbox_loglik(data, v, a, z, t, err=1e-8):
    """Create a custom blackbox likelihood function."""
    data = data[:, 0] * data[:, 1]
    data_nrows = data.shape[0]
    # Our function expects inputs as float64, but they are not guaranteed to
    # come in as such --> we type convert
    return hddm_wfpt.wfpt.wiener_logp_array(
        np.float64(data),
        (np.ones(data_nrows) * v).astype(np.float64),
        np.ones(data_nrows) * 0,
        (np.ones(data_nrows) * 2 * a).astype(np.float64),
        (np.ones(data_nrows) * z).astype(np.float64),
        np.ones(data_nrows) * 0,
        (np.ones(data_nrows) * t).astype(np.float64),
        np.ones(data_nrows) * 0,
        err,
        1,
    )
def my_blackbox_loglik(data, v, a, z, t, err=1e-8):
    """Create a custom blackbox likelihood function."""
    data = data[:, 0] * data[:, 1]
    data_nrows = data.shape[0]
    # Our function expects inputs as float64, but they are not guaranteed to
    # come in as such --> we type convert
    return hddm_wfpt.wfpt.wiener_logp_array(
        np.float64(data),
        (np.ones(data_nrows) * v).astype(np.float64),
        np.ones(data_nrows) * 0,
        (np.ones(data_nrows) * 2 * a).astype(np.float64),
        (np.ones(data_nrows) * z).astype(np.float64),
        np.ones(data_nrows) * 0,
        (np.ones(data_nrows) * t).astype(np.float64),
        np.ones(data_nrows) * 0,
        err,
        1,
    )

Define HSSM class with our Blackbox Likelihood¶

We can now define our HSSM model class as usual, however passing our my_blackbox_loglik() function to the loglik argument, and passing as loglik_kind = blackbox.

The rest of the model config is as usual. Here we can reuse our ddm model config, and simply specify bounds on the parameters (e.g. your Blackbox Likelihood might be trustworthy only on a restricted parameters space).

In [103]:

Copied!





blackbox_model = hssm.HSSM(
    data=dataset_blackbox,
    model="ddm",
    loglik=my_blackbox_loglik,
    loglik_kind="blackbox",
    model_config={
        "bounds": {
            "v": (-10.0, 10.0),
            "a": (0.5, 5.0),
            "z": (0.0, 1.0),
        }
    },
    t=bmb.Prior("Uniform", lower=0.0, upper=2.0),
)
blackbox_model = hssm.HSSM(
    data=dataset_blackbox,
    model="ddm",
    loglik=my_blackbox_loglik,
    loglik_kind="blackbox",
    model_config={
        "bounds": {
            "v": (-10.0, 10.0),
            "a": (0.5, 5.0),
            "z": (0.0, 1.0),
        }
    },
    t=bmb.Prior("Uniform", lower=0.0, upper=2.0),
)

{'t_interval__': array(0., dtype=float32), 'a_interval__': array(0., dtype=float32), 'z_interval__': array(0., dtype=float32), 'v': array(0., dtype=float32)}

In [104]:

Copied!

sample = blackbox_model.sample()
sample = blackbox_model.sample()

Using default initvals.

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>Slice: [t]
>Slice: [a]
>Slice: [z]
>Slice: [v]

Output()

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 24 seconds.

Output()

CLEANING RESULTS
MAIN CLEANUP LOOP
RUNNING COMPONENT <bambi.backend.model_components.DistributionalComponent object at 0x31b04f1d0>
PERFORMING PREDICTION

NOTE:

Since Blackbox likelihood functions are assumed to not be differentiable, our default sampler for such likelihood functions is a Slice sampler. HSSM allows you to choose any other suitable sampler from the PyMC package instead. A bunch of options are available for gradient-free samplers.

Results¶

In [105]:

Copied!

az.summary(sample)
az.summary(sample)

Out[105]:

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
a	1.541	0.031	1.485	1.600	0.001	0.001	1363.0	2047.0	1.0
t	0.480	0.024	0.434	0.523	0.001	0.001	1136.0	1445.0	1.0
v	0.582	0.033	0.521	0.645	0.001	0.001	1249.0	1777.0	1.0
z	0.477	0.013	0.451	0.500	0.000	0.000	1079.0	1486.0	1.0

In [106]:

Copied!





az.plot_trace(
    sample,
    lines=[(key_, {}, param_dict_blackbox[key_]) for key_ in param_dict_blackbox],
)
plt.tight_layout()
az.plot_trace(
    sample,
    lines=[(key_, {}, param_dict_blackbox[key_]) for key_ in param_dict_blackbox],
)
plt.tight_layout()

HSSM Random Variables in PyMC¶

We covered a lot of ground in this tutorial so far. You are now a sophisticated HSSM user.

It is therefore time to reveal a secret. We can actuallly peel back one more layer...

Instead of letting HSSM help you build the entire model, we can instead use HSSM to construct valid PyMC distributions and then proceed to build a custom PyMC model by ourselves...

We will illustrate the simplest example below. It sets a pattern that can be exploited for much more complicated modeling exercises, which importantly go far beyond what our basic HSSM class may facilitate for you!

See the dedicated tutorial in the documentation if you are interested.

Let's start by importing a few convenience functions:

In [107]:

Copied!

# DDM models (the Wiener First-Passage Time distribution)
from hssm.distribution_utils import make_distribution
from hssm.likelihoods import DDM
# DDM models (the Wiener First-Passage Time distribution)
from hssm.distribution_utils import make_distribution
from hssm.likelihoods import DDM

Simulate some data¶

In [108]:

Copied!

# Simulate
param_dict_pymc = dict(v=0.5, a=1.5, z=0.5, t=0.5, theta=0.0)

dataset_pymc = hssm.simulate_data(model="ddm", theta=param_dict_pymc, size=1000)
# Simulate
param_dict_pymc = dict(v=0.5, a=1.5, z=0.5, t=0.5, theta=0.0)

dataset_pymc = hssm.simulate_data(model="ddm", theta=param_dict_pymc, size=1000)

Build a custom PyMC Model¶

We can now use our custom random variable DDM directly in a PyMC model.

In [109]:

Copied!





import pymc as pm

with pm.Model() as ddm_pymc:
    v = pm.Uniform("v", lower=-10.0, upper=10.0)
    a = pm.HalfNormal("a", sigma=2.0)
    z = pm.Uniform("z", lower=0.01, upper=0.99)
    t = pm.Uniform("t", lower=0.0, upper=0.6)

    ddm = DDM(
        "DDM", v=v, a=a, z=z, t=t, observed=dataset_pymc[["rt", "response"]].values
    )
import pymc as pm

with pm.Model() as ddm_pymc:
    v = pm.Uniform("v", lower=-10.0, upper=10.0)
    a = pm.HalfNormal("a", sigma=2.0)
    z = pm.Uniform("z", lower=0.01, upper=0.99)
    t = pm.Uniform("t", lower=0.0, upper=0.6)

    ddm = DDM(
        "DDM", v=v, a=a, z=z, t=t, observed=dataset_pymc[["rt", "response"]].values
    )

Let's check the model graph:

In [110]:

Copied!

pm.model_to_graphviz(model=ddm_pymc)
pm.model_to_graphviz(model=ddm_pymc)

Out[110]:

Looks remarkably close to our HSSM version!

We can use PyMC directly to sample and finally return to ArviZ for some plotting!

In [111]:

Copied!

with ddm_pymc:
    ddm_pymc_trace = pm.sample()
with ddm_pymc:
    ddm_pymc_trace = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [v, a, z, t]

Output()

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 16 seconds.

In [112]:

Copied!





az.plot_trace(
    ddm_pymc_trace,
    lines=[(key_, {}, param_dict_pymc[key_]) for key_ in param_dict_pymc],
)

plt.tight_layout()
az.plot_trace(
    ddm_pymc_trace,
    lines=[(key_, {}, param_dict_pymc[key_]) for key_ in param_dict_pymc],
)

plt.tight_layout()

In [113]:

Copied!

az.plot_forest(ddm_pymc_trace)
az.plot_forest(ddm_pymc_trace)

Out[113]:

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

Alternative Models with PyMC¶

With very little extra work, we can in fact load any of the models accessible via HSSM. Here is an example, where we load the angle model instead.

We first construction the likelihood function, using make_likelihood_callable().

Then we produce a valid pymc.distribution using the make_distribution() utility function.

Just like the DDM class above, we can then use this distribution inside a PyMC model.

In [114]:

Copied!





from hssm.distribution_utils import make_likelihood_callable

angle_loglik = make_likelihood_callable(
    loglik="angle.onnx",
    loglik_kind="approx_differentiable",
    backend="jax",
    params_is_reg=[0, 0, 0, 0, 0],
)

ANGLE = make_distribution(
    "angle",
    loglik=angle_loglik,
    list_params=hssm.defaults.default_model_config["angle"]["list_params"],
)
from hssm.distribution_utils import make_likelihood_callable

angle_loglik = make_likelihood_callable(
    loglik="angle.onnx",
    loglik_kind="approx_differentiable",
    backend="jax",
    params_is_reg=[0, 0, 0, 0, 0],
)

ANGLE = make_distribution(
    "angle",
    loglik=angle_loglik,
    list_params=hssm.defaults.default_model_config["angle"]["list_params"],
)

Note that we need to supply the params_is_reg argument ("reg" for "regression"). This is a boolean vector, which specifies for each input to the likelihood function, whether or not it is defined to be "trial-wise", as is expected if the parameter is the output e.g. of a regression function.

In [115]:

Copied!





import pymc as pm

# Angle pymc
with pm.Model() as angle_pymc:
    # Define parameters
    v = pm.Uniform("v", lower=-10.0, upper=10.0)
    a = pm.Uniform("a", lower=0.5, upper=2.5)
    z = pm.Uniform("z", lower=0.01, upper=0.99)
    t = pm.Uniform("t", lower=0.0, upper=0.6)
    theta = pm.Uniform("theta", lower=-0.1, upper=1.0)

    # Our RV
    angle = ANGLE(
        "DDM",
        v=v,
        a=a,
        z=z,
        t=t,
        theta=theta,
        observed=dataset_pymc[["rt", "response"]].values,
    )
import pymc as pm

# Angle pymc
with pm.Model() as angle_pymc:
    # Define parameters
    v = pm.Uniform("v", lower=-10.0, upper=10.0)
    a = pm.Uniform("a", lower=0.5, upper=2.5)
    z = pm.Uniform("z", lower=0.01, upper=0.99)
    t = pm.Uniform("t", lower=0.0, upper=0.6)
    theta = pm.Uniform("theta", lower=-0.1, upper=1.0)

    # Our RV
    angle = ANGLE(
        "DDM",
        v=v,
        a=a,
        z=z,
        t=t,
        theta=theta,
        observed=dataset_pymc[["rt", "response"]].values,
    )

In [116]:

Copied!

with angle_pymc:
    idata_object = pm.sample(nuts_sampler="numpyro")
with angle_pymc:
    idata_object = pm.sample(nuts_sampler="numpyro")

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

In [117]:

Copied!

az.plot_trace(
    idata_object, lines=[(key_, {}, param_dict_pymc[key_]) for key_ in param_dict_pymc]
)

plt.tight_layout()
az.plot_trace(
    idata_object, lines=[(key_, {}, param_dict_pymc[key_]) for key_ in param_dict_pymc]
)

plt.tight_layout()

Regression via PyMC¶

Finally to illustrate the usage of PyMC a little more elaborately, let us build a PyMC model with regression components.

In [118]:

Copied!





from typing import Optional


def make_params_is_reg_vec(
    reg_parameters: Optional[list] = None, parameter_names: Optional[list] = None
):
    """Make a list of Trues and Falses to indicate which parameters are vectors."""
    if (not isinstance(reg_parameters, list)) or (
        not isinstance(parameter_names, list)
    ):
        raise ValueError("Both reg_parameters and parameter_names should be lists")

    bool_list = [0] * len(parameter_names)
    for param in reg_parameters:
        bool_list[parameter_names.index(param)] = 1
    return bool_list
from typing import Optional


def make_params_is_reg_vec(
    reg_parameters: Optional[list] = None, parameter_names: Optional[list] = None
):
    """Make a list of Trues and Falses to indicate which parameters are vectors."""
    if (not isinstance(reg_parameters, list)) or (
        not isinstance(parameter_names, list)
    ):
        raise ValueError("Both reg_parameters and parameter_names should be lists")

    bool_list = [0] * len(parameter_names)
    for param in reg_parameters:
        bool_list[parameter_names.index(param)] = 1
    return bool_list

In [119]:

Copied!





# Set up trial by trial parameters
v_intercept_pymc_reg = 0.3
x_pymc_reg = np.random.uniform(-1, 1, size=1000)
v_x_pymc_reg = 0.8
y_pymc_reg = np.random.uniform(-1, 1, size=1000)
v_y_pymc_reg = 0.3
v_pymc_reg = v_intercept + (v_x * x) + (v_y * y)

param_dict_pymc_reg = dict(
    v_Intercept=v_intercept_pymc_reg,
    v_x=v_x_pymc_reg,
    v_y=v_y_pymc_reg,
    v=v_pymc_reg,
    a=1.5,
    z=0.5,
    t=0.1,
    theta=0.0,
)

# base dataset
pymc_reg_data = hssm.simulate_data(model="ddm", theta=param_dict_pymc_reg, size=1)

# Adding covariates into the datsaframe
pymc_reg_data["x"] = x
pymc_reg_data["y"] = y

# Make the boolean vector for params_is_reg argument
bool_param_reg = make_params_is_reg_vec(
    reg_parameters=["v"],
    parameter_names=hssm.defaults.default_model_config["angle"]["list_params"],
)

angle_loglik = make_likelihood_callable(
    loglik="angle.onnx",
    loglik_kind="approx_differentiable",
    backend="jax",
    params_is_reg=bool_param_reg,
)

ANGLE = make_distribution(
    "angle",
    loglik=angle_loglik,
    list_params=hssm.defaults.default_model_config["angle"]["list_params"],
)
# Set up trial by trial parameters
v_intercept_pymc_reg = 0.3
x_pymc_reg = np.random.uniform(-1, 1, size=1000)
v_x_pymc_reg = 0.8
y_pymc_reg = np.random.uniform(-1, 1, size=1000)
v_y_pymc_reg = 0.3
v_pymc_reg = v_intercept + (v_x * x) + (v_y * y)

param_dict_pymc_reg = dict(
    v_Intercept=v_intercept_pymc_reg,
    v_x=v_x_pymc_reg,
    v_y=v_y_pymc_reg,
    v=v_pymc_reg,
    a=1.5,
    z=0.5,
    t=0.1,
    theta=0.0,
)

# base dataset
pymc_reg_data = hssm.simulate_data(model="ddm", theta=param_dict_pymc_reg, size=1)

# Adding covariates into the datsaframe
pymc_reg_data["x"] = x
pymc_reg_data["y"] = y

# Make the boolean vector for params_is_reg argument
bool_param_reg = make_params_is_reg_vec(
    reg_parameters=["v"],
    parameter_names=hssm.defaults.default_model_config["angle"]["list_params"],
)

angle_loglik = make_likelihood_callable(
    loglik="angle.onnx",
    loglik_kind="approx_differentiable",
    backend="jax",
    params_is_reg=bool_param_reg,
)

ANGLE = make_distribution(
    "angle",
    loglik=angle_loglik,
    list_params=hssm.defaults.default_model_config["angle"]["list_params"],
)

In [120]:

Copied!





import pytensor.tensor as pt

with pm.Model(
    coords={
        "idx": pymc_reg_data.index,
        "resp": ["rt", "response"],
        "features": ["x", "y"],
    }
) as pymc_model_reg:
    # Features
    x_ = pm.Data("x", pymc_reg_data["x"].values, dims="idx")
    y_ = pm.Data("y", pymc_reg_data["y"].values, dims="idx")
    # Target
    obs = pm.Data("obs", pymc_reg_data[["rt", "response"]].values, dims=("idx", "resp"))

    # Priors
    a = pm.Uniform("a", lower=0.5, upper=2.5)
    z = pm.Uniform("z", lower=0.01, upper=0.99)
    t = pm.Uniform("t", lower=0.0, upper=0.6)
    theta = pm.Uniform("theta", lower=-0.1, upper=1.0)
    v_Intercept = pm.Uniform("v_Intercept", lower=-3, upper=3)
    v_betas = pm.Normal("v_beta", mu=[0, 0], sigma=0.5, dims=("features"))

    # Regression equation
    v = pm.Deterministic(
        "v", v_Intercept + pt.stack([x_, y_], axis=1) @ v_betas, dims="idx"
    )

    # Our RV
    angle = ANGLE(
        "angle",
        v=v.squeeze(),
        a=a,
        z=z,
        t=t,
        theta=theta,
        observed=obs,
        dims=("idx", "resp"),
    )
import pytensor.tensor as pt

with pm.Model(
    coords={
        "idx": pymc_reg_data.index,
        "resp": ["rt", "response"],
        "features": ["x", "y"],
    }
) as pymc_model_reg:
    # Features
    x_ = pm.Data("x", pymc_reg_data["x"].values, dims="idx")
    y_ = pm.Data("y", pymc_reg_data["y"].values, dims="idx")
    # Target
    obs = pm.Data("obs", pymc_reg_data[["rt", "response"]].values, dims=("idx", "resp"))

    # Priors
    a = pm.Uniform("a", lower=0.5, upper=2.5)
    z = pm.Uniform("z", lower=0.01, upper=0.99)
    t = pm.Uniform("t", lower=0.0, upper=0.6)
    theta = pm.Uniform("theta", lower=-0.1, upper=1.0)
    v_Intercept = pm.Uniform("v_Intercept", lower=-3, upper=3)
    v_betas = pm.Normal("v_beta", mu=[0, 0], sigma=0.5, dims=("features"))

    # Regression equation
    v = pm.Deterministic(
        "v", v_Intercept + pt.stack([x_, y_], axis=1) @ v_betas, dims="idx"
    )

    # Our RV
    angle = ANGLE(
        "angle",
        v=v.squeeze(),
        a=a,
        z=z,
        t=t,
        theta=theta,
        observed=obs,
        dims=("idx", "resp"),
    )

In [121]:

Copied!





with pymc_model_reg:
    idata_pymc_reg = pm.sample(
        nuts_sampler="numpyro", idata_kwargs={"log_likelihood": True}
    )
with pymc_model_reg:
    idata_pymc_reg = pm.sample(
        nuts_sampler="numpyro", idata_kwargs={"log_likelihood": True}
    )

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

  0%|          | 0/2000 [00:00<?, ?it/s]

In [122]:

Copied!

az.plot_forest(idata_pymc_reg, var_names=["~v"])
az.plot_forest(idata_pymc_reg, var_names=["~v"])

Out[122]:

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

All layers peeled back, the only limit in your modeling endeavors becomes the limit of the PyMC universe!

Enjoy the exploration!

Colab Instructions¶

Basic Imports¶

Data Simulation¶

Using simulate_data()¶

Using ssm-simulators¶

ArviZ for Plotting¶

Main Tutorial¶

Initial Dataset¶

First HSSM Model¶

Instantiate the model¶

Model Graph¶

Sample from the Model¶

Inference Data / What gets returned from the sampler?¶

Basic Manipulation¶

Accessing groups and variables¶

Combine chain and draw dimension¶

Making use of ArviZ¶

Summary table¶

Trace plot¶

Forest Plot¶

Combining Chains¶

Basic Marginal Posterior Plot¶

Posterior Pair Plot¶

Compute Quantities from idata¶

Example: Mean and Covariance of Posterior Parameters¶

HSSM Model based on LAN likelihood¶

Simulating Angle Data¶

Choosing Priors¶

Fixing a parameter to a given value¶

Named priors¶

HSSM Model with Regression¶

Case 1: One parameter is a Regression Target¶

Simulating Data¶

Basic Model¶

Param class¶

Custom Model¶

Case 2: One parameter is a Regression (LAN)¶

Case 3: Multiple Parameters are Regression Targets (LAN)¶

Case 4: Categorical covariates¶

Hierarchical Inference¶

Simulate Data¶

Basic Hierarchical Model¶

Model Comparison¶

Scenario¶

Data Simulation¶

Defining the Models¶

Compare¶

Closer look!¶

'Blackbox' Likelihoods¶

What is a Blackbox Likelihood Function?¶

Simulating simple dataset from the DDM¶

Define the likelihood¶

Define HSSM class with our Blackbox Likelihood¶

Results¶

HSSM Random Variables in PyMC¶

Simulate some data¶

Build a custom PyMC Model¶

Alternative Models with PyMC¶

Regression via PyMC¶

End¶

Using `simulate_data()`¶

Using `ssm-simulators`¶

Combine `chain` and `draw` dimension¶

`Param` class¶